ЭТАПЫ ОБРАЩЕНИЯ ИНФОРМАЦИИ

 

ВВЕДЕНИЕ

Возникновение теории информации связывают обычно с появлением фундаментальной работы американского ученого К.Шеннона «Математическая теория связи» (1948). Однако в теорию информации органически вошли и результаты, полученные другими учеными, например Р. Хартли, впервые предложившим количественную меру информации (1928), акад. В. А. Котельниковым, сформулировавшим важнейшую теорему о возможности представления непрерывной функции совокупностью ее значений в отдельных точках отсчета (1933) и разработавшим оптимальные методы приема сигналов на фоне помех (1946), акад. А. Н. Колмогоровым, внесшим огромный вклад в статистическую теорию колебаний, являющуюся математиче­ской основой теории информации (1941).

В последующие годы теория информации получила дальнейшее развитие в трудах советских ученых (А. Н. Колмогорова, А. Я. Хинчина, В. И. Сифорова,- Р. Л. Добрушина, М. С. Пинскера, А. Н. Железнова, Л. М. Финка и др.), а также ряда зарубежных ученых (В. Макмиллана, А. Файнстейна, Д. Габора, Р. М. Фа но, Ф. М. Вудворта, С. Гольдмана, Л. Бриллюэна и др.).

К теории информации в ее узкой классической постановке относят результаты решения ряда фундаментальных теоретических вопросов, касающихся повышения эффективности функционирования систем связи. Это в первую очередь:

-анализ сигналов как средства передачи сообщений, включающий вопросы оценки переносимого ими «количества информации»;

-анализ информационных характеристик источников, сообщений и каналов связи и обоснование принципиальной возможности кодирования и декодирования сообщений, обеспечивающих предельно допустимую скорость передачи сообщений по каналу связи как при отсутствии, так и при наличии помех.

-анализ источников искажения передаваемой информации и выделение сигнала из шума

При более широкой трактовке теории информации результаты рассмотрения указанных вопросов составляют ее основу. Совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации.

Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В этом случае к ней относят все локальные проблемы систем связи, включая, например, проблему оптимального приема и др.

В соответствии с третьей крайней точкой зрения к компетенции теории информации относят все проблемы и задачи, в формулировку которых входит понятие информации. Ее предметом считают изучение процессов, связанных с получением, передачей, хранением, обработкой и использованием информации. В такой постановке она затрагивает проблемы многих наук (в частности, кибернетики, биологии, психологии, лингвистики, педагогики) на всех уровнях (синтактическом, семантическом и прагматическом).

В основе своей эта теория математическая. Основные ее понятия (энтропия, количество информации, пропускная способность) определяются только через вероятности событий, которым может быть приписано самое различное физическое содержание. Подход к исследованиям в других областях науки с позиций использования основных идей теории информации получил название теоретико-информационного подхода. Понятие «информация» является центральным понятием кибернетики. Оно используется и в теории информации, хотя основным понятием классической теории информации следует признать «количество информации», смысла которого коснемся несколько позже.

Имеется множество определений понятия информации от наиболее общего философского (информация есть отражение реального мира) до наиболее узкого практического (информация есть все сведения, являющиеся объектом хранения, передачи и преобразования). Информацию следует рассматривать как свойство объекта в потенциальном смысле — свойство, которое проявляется лишь при взаимодействии объектов (процессов).

При всех различиях в трактовке понятия информации бесспорно то, что проявляется информация всегда в материально-энергетической форме в виде сигналов. Информацию, представленную в формализованном виде, позволяющем осуществить ее обработку с помощью технических средств, называют данными.

 

ЭТАПЫ ОБРАЩЕНИЯ ИНФОРМАЦИИ

При обращении информации в системах можно выделить отдельные этапы. Так как материальным носителем информации является сигнал, то реально это будут этапы обращения и преобразования сигналов (рис.1).

На этапе восприятия информации осуществляется целенаправленное извлечение и анализ информации о каком-либо объекте (процессе), в результате чего формируется образ объекта, проводятся его опознание и оценка. При этом необходимо отделить интересующую нас в данном случае информацию от мешающей. Простейшим видом восприятия является различение двух противоположных состояний: наличия («да») и отсутствия («нет»), более сложным — измерение.

На этапе подготовки информации проводятся такие операции, как нормализация, аналого-цифровое преобразование, шифрование. В результате восприятия и подготовки получается сигнал в форме, удобной для передачи или обработки.

На этапах передачи и хранения информация пересылается либо из одного места в другое, либо от одного момента времени до другого. Для передачи на расстояние используются каналы различной физической природы, самыми распространенными из которых являются электрические и электромагнитные. Для хранения информации используются в основном полупроводниковые, оптические и магнитные носители. Извлечение сигнала на выходе канала, подверженного действию шумов, носит характер вторичного восприятия.

На этапах обработки информации выявляются ее общие и существенные взаимозависимости, представляющие интерес для системы. Преобразование информации на этапе обработки (как и на других этапах) осуществляется либо средствами информационной техники, либо человеком. Если процесс обработки формализуем, он может выполняться техническими средствами. В современных сложных системах эти функции возлагаются на ЭВМ и микропроцессоры. Если процесс обработки не поддается формализации и требует творческого подхода, обработка информации осуществляется человеком. В системах управления важнейшей целью обработки является решение задачи выбора управляющих воздействий (этап принятия решения).

Этап отображения информации должен предшествовать этапам, связанным с участием человека. Цель этапа отображения — предоставить человеку нужную ему информацию с помощью устройств, способных воздействовать на его органы чувств.

На этапе воздействия информация используется для осуществления необходимых изменений в системе.

 

СИСТЕМА ПЕРЕДАЧИ ИНФОРМАЦИИ

Структурная схема одноканальной системы передачи информации приведена на рисунке. Информация поступает в систему в форме сообщений. Под сообщением… Различают дискретные и непрерывные сообщения. Дискретные сообщения формируются в результате последовательной выдачи источником отдельных элементов — знаков.…

КОЛИЧЕСТВО ИНФОРМАЦИИ

Информация проявляется всегда в форме сигналов. Сигналы z, поступающие с выхода первичного преобразователя источника информации на вход канала… Отдельные первичные сигналы с выхода источника дискретных сообщений называют… Основное понятие теории информации — количество информации — рассматривается в данном параграфе применительно к…

Передача информации от дискретного источника.

Вследствие воздействия помех полученный элемент сообщения в общем случае отличается от переданного. Подчеркнем это различие. Обозначив принимаемые… Априорная неопределенность (неопределенность до получения элемента сообщения)…

Передача информации от непрерывного источника.

Для источника, имеющего непрерывное множество состояний, среднее количество информации, содержащееся в каждом принятом значении случайной величины W… Соотношение несложно выразить в виде:

Свертки

В одном измерении интеграл свертки двух функций f(х)и g(х) определяется как: (2.4)

Свойства фурье-преобразований

можно переписать следующим образом: (2.16)

Умножение и свертка

  (2.29)  

Пространство и время

Кроме связи между пространственными распределениями f(r) и амплитудами дифракции F(u), фурье-преобразование также связывает изменение функции во… (2.31)

Фурье-преобразование в оптике

Для того, чтобы ознакомится с использованием обычных фурье-преобразований и показать, как они используются при рассмотрении кинематической дифракции, приведем ряд примеров, в которых используются обе рассмотренные функции. При рассмотрении дифракции в большинстве случаев будем исходить из простых одно- или двумерных объектов.

 

Точечный источник или точечная апертура

Распределение амплитуды при рассеянии от очень малого ис­точника или при прохождении через очень малую апертуру (или щель) в одном измерении можно…  

Обратное рассмотренному в разделе 2.3.1

 

Фурье-преобразование плоской волны (1.8) относительно толь­ко переменной t дает:

(2.34)

 

т.е. дельта-функцию для частоты и плоскую волну в реальном пространстве. Фурье-преобразование относительно переменной х дает :

(2.35)

 

т.е. синусоидальное изменение во времени и дельта-функцию в обратном пространстве. Преобразование относительно обеих пе­ременных дает :

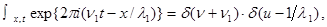
(2.36)

 

что является дельта-функцией как для частоты, так и в обратном пространстве.

Если взять фурье-преобразование всех возможных волн, ко­торые могут существовать в данной среде относительно х и t, то получим набор точек, определяющих соотношение между час­тотой n и l^-1 (или между угловой частотой w и k), известное под названием дисперсионного соотношения для такого типа волны и определенной среды.

 

 

Трансляция объекта

Трансляция объекта описывается выражением   (2.37)

Функция щели

Функция прохождения для щели шириной a в непрозрачном экране дается выражением:  

Другая форма функции щели

Проиллюстрируем использование выражения (2.27). Заметим при этом, что для функции щели, которая была определена в разд. 2.3.4, справедливо…  

Прямолинейный край

  Для прямолинейного края функция прохождения имеет вид:

Обобщение преобразований Фурье. Преобразования Лапласа

Умножим некоторое заданное колебание u(t) на e-ct, где с — положительная константа, выбранная так, чтобы колебание u(t)e-c удовлетворяло условию… Обеспечить существование этого интеграла можно, задавая все колебания u(t)…  

Теорема о преобразовании суммы колебаний (теорема о линейности)

Это теорема справедлива и для суммы любого количества колебаний.

Теорема о6 умножении на константу Если L u (t) I = U (р) и а — константа, то

Теорема о запаздывании колебания u(t)

 

 

Если L[u(t)] = U(p), то

т. е. изображение импульса, возникшего на t позже, можно найти, умножив изображение исходного импульса на е~^рt.

Теорема о преобразовании производной от колебания

Если L[u(t)] = U(p), то

где и (0 +) — значение колебания при t = 0 и приближении к нулю справа (это существенно при скачке функции u(t) в начале коорди­нат).

Повторно применяя формулу , можно распространить теорему на производные более высоких порядков.

Теорема о преобразовании интеграла колебания

Если L[u(t)]^=U(p), то

где u^-1 (0 +) — значение интеграла колебания u(f), когда t = 0, при приближении к нулю справа.

Теорема об изменении масштаба времени колебания

Если L[u (t)]=U(p), a a=const>0, то

 

Теорема о преобразовании свертки функций

Если L[и₁ (t)] = U₁ (р) и L[u₂(t)]=U₂(p), то

 

 

Операция образования величины

  часто встречается при расчете радиотехнических процессов и называется сверткой функций uL(t) и u2(t).

Теорема об умножении колебания на показательную функцию

Если L [и (t)] = U (р) и а — действительное или комплексное число с положительной частью, то

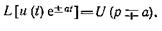
Теорема о преобразовании колебания с переменной амплитудой

Если

и

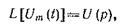то

 

 

Вследствие широкого применения колебаний эта теорема особенно важна. Рассмотрим ее подробнее применительно к преобразованиям Фурье. Пусть

 

 

Тогда согласно теореме

 

 

где G_u (w) — спектральная функция экспоненциального импульса Ee^-at,

 

Подставляя (1.45) в (1.44), получим

 

 

 

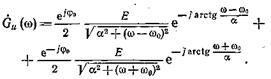
На рис. приведены графики модуля спектральной функции амплитуды (1.45) и модулей обоих слагаемых (1.46). Для получения последних необходимо, как это следует из (1.44), сместить графики спектральной функции огибающей по оси частот на w_о и - w₀ и уменьшить их ординаты в два раза.

Некоторые соотношения между колебаниями и их спектрами

 

Представления колебаний рядом и интегралом Фурье находят на практике широкое применение. Рассмотрим некоторые важные соотношения, которые имеют место при этом.

Выражение энергии колебания через его спектральную функцию. Спектральная плотность энергии

Изменяя порядок интегрирования, получим

Энергия взаимодействия двух колебаний

На основании (1.53) и теоремы о линейности преобразований Фурье  

Соотношение между длительностью колебанияи шириной его спектра. Определения длительности колебания

   

Равномерное распределение.

  Функцию распределения находят путем интегрирования:

Математическое ожидание

 

 

естественно, совпадает с центром отрезка [х₁, х₂].

Как легко проверить, дисперсия случайной величины, имеющей равномерное распределение вероятности,

 

Гауссово (нормальное) распределение.

(6.9)   содержащая два числовых параметра m и s. График данной функции представляет собой колоколообразную кривую с…

Плотность вероятности функции от случайной величины.

px(x)dx = py(y) |dy|. Отсюда Рy (y) = Рx(х) || = Px[g (у)]|| , (6.11) ,

Функция распределения и плотность вероятности.

  Отвечающая ей n-мерная плотность вероятности p(x1, х2,…, хn) удовлетворяет соотношению

Корреляция.

Может оказаться, что изображающие точки в среднем располагаются вдоль некоторой прямой, так что в каждом отдельном испытании величины х1 и х2 имеют… Однако возможен случай хаотического расположения точек на плоскости. Говорят,… Количественной характеристикой степени статистической связи двух случайных величин служит их ковариационный момент К12…

Функциональные преобразования многомерных случайных величин.

   

Стационарные случайные процессы

Среди случайных процессов особое место занимают стационар­ные случайные процессы, имеющие важное значение при рас­смотрении большого числа задач.… При определенных условиях, математическая формулировка которых здесь не будет… Обозначая среднее значение по времени через |, можно напи­сать

Квазидетерминированные процессы и случайные процессы

В то же время при рассмотрении многих радиотехнических задач возможно ограничиться менее общими предположениями о характере сигнала и принять, что… Удобная для применений модель квазидетерминированного сигнала может быть…  

ПОМЕХИ РАДИОПРИЕМУ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ

Предварительные замечания

Здесь e(t) — передаваемый сигнал; k{t) — коэффициент, харак­теризующий…  

Виды помех

По законам распределения разделяют помехи на гауссовские и негауссовские. Такое разделение удобно вследствие того, что значительная часть наиболее… Хотя для реальной помехи энергетический спектр существенно зависит от частоты,… По характеру стационарности различают помехи стационарные и нестационарные. Как уже отмечалось в гл. 1, случайный…

Зависимость уровня помех от частоты

Космические шумы, действующие на входе наземных радио­приемников, находятся в частотном диапазоне примерно 10МГц... ... 10 ГГц. На частотах ниже 10…  

Законы распределения помех

Флуктуационные помехи являются стационарными и, как уже отмечалось, характеризуются гауссовскнм (нормальным) законом распределения, при котором…  

Случайные процессы как математические модели реальных помех

В настоящем параграфе не рассматриваются вопросы о том, какие элементы должны быть включены в приемный тракт для того, чтобы обеспечить… Чтобы выполнить анализ прохождения помех через приемный тракт и рассмотреть… выбранный вид случайного процесса должен быть пригоден для описания возможно более широкого класса помех…

Марковские процессы

Теория марковских случайных процессов и применение этой теории для аппроксимации радиопомех изложены в [1, 3, 4]. В § 2.7—2.9 настоящей главы… Флуктуационные помехи можно считать частным случаем марков­ской модели…

Флуктуационные помехи

Важнейшими характеристиками флуктуационного процесса яв­ляются корреляционная (ковариационная) функция и спектраль­ная плотность. Определим… При увеличении т зависимости между l{t+%) и £(f) уменьша­ются, и при т->-оо эти величины становятся…

Спектральная плотность флуктуационных помех

Корреляционная функция центрированного флуктуационного процесса |ц(0=1(0—mi и спектральная плотность g(f) связаны между собой парой преобразований…     Для случая, когда т = 0, вместо (2.16) получим

Белый шум

Спектральная плотность (энергетический спектр) белого шума g(f) не ограничена по частоте и имеет постоянную величину где No — мощность шума в пределах единичной полосы в 1 Гц.

ТЕПЛОВЫЕ ШУМЫ

   

ДРОБОВОЙ ШУМ

Для определения среднего квадрата этих флуктуации необходимо учесть, что процесс вылета электронов при термоионной эмиссии является пуассоновским.…    

ГЕНЕРАЦИОННО-РЕКОМБИНАЦИОННЫЙ ШУМ

  где функции g(N) и r(N), характеризующие соответственно скорости генерации и рекомбинации носителей, являются…

ПРИНЦИП ВЫДЕЛЕНИЯ СИГНАЛА ИЗ ШУМА

Спектр сигнала обычно узкополосный и занимает некоторый интервал частот Df. Спектр гауссовского шума равномерен во всем диапазоне частот. Мощность… Время измерения связано с шириной полосы пропускания обратной зависимостью…

СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ

Если какой-либо сигнал представлен в виде суммы гармонических колебаний с различными частотами, то говорят, что осуществлено спектральное разложение… Математической моделью процесса, циклически повторяющегося во времени является… , (1.1)

Ряды Фурье.

, , , (1.2)

Преобразование Фурье.

Периодическое продолжение импульса. Пусть - импульсный сигнал, длительность которого конечна. Дополнив мысленно его такими же сигналами,… (1.10) с коэффициентами

Понятие спектральной плотности сигнала.

Воспользуемся тем, что коэффициенты ряда Фурье образуют комплексно-сопряженные пары: ; .

Обратное преобразование Фурье.

Предположим вновь, что непериодический сигнал получается из периодической последовательности, когда её период устремится к бесконечности.… . Коэффициент пропорционален разности между частотами соседних гармоник:

Преобразование Лапласа.

Естественное обобщение этого принципа состоит в том, что вместо комплексных экспоненциальных сигналов с чисто мнимыми показателями вводят в… , получившее название комплексной частоты.

Условия существования преобразования Лапласа. Связь между преобразованиями Фурье и Лапласа.

. (1.18) Сигнал f(t) называется оригиналом, а функция F(p) – его изображением. Условие существования интеграла (1.18) заключается в следующем: сигнал f(t) должен иметь не более чем экспоненциальную…

Представление отклика линейной цепи в форме интеграла наложения или свертки.

  Любой детерминированный сигнал можно представить при помощи единичной… Единичная ступенька (скачок, функция включения, или функция Хевисайда) определяется аналитически

Дискретное представление сигналов. Теорема Котельникова.

  Если в спектре сигнала нет составляющих с частотой выше , то такая частота… при .

Прохождение сигналов через линейные системы.

В наиболее простом случае, как входной сигнал uвх(t) так и выходной сигнал uвых(t),называемый также откликом или выходной реакцией системы,… вх а выходной сигнал – в виде n-мерного вектора

Импульсные, переходные и частотные характеристики линейных систем.

Замечательная особенность линейных систем – справедливость принципа суперпозиции – открывает прямой путь к систематическому решению задач о… Такой анализ основан на временном представлении свойств сигналов и систем. В… Импульсной характеристикой системы называется функция , являющаяся откликом системы на входной сигнал . Это означает,…

Вход Выход Вход Выход

а) б) Рисунок 5. Схемы линейных систем: а – линейная колебательная система с…  

ДИАГРАММА НАПРАВЛЕННОСТИ ИЗЛУЧАЮЩЕЙ СИСТЕМЫ

Пространственное распределение напряжённости излучаемого антенной поля можно описать некоторой функцией. Такая функция называется диаграммой… Линейные антенны подобно линейным цепям удовлетворяют принципу взаимности. Как…  

Характеристики диаграмм направленности.

Относительный уровень боковых максимумов есть отношение напряжённости поля или интенсивности излучения в направлении боковых максимумов к… Ширина главного лепестка 2θ по полярным диаграммам определяется углом… Ширина главного лепестка 2θ по прямоугольным диаграммам направленности определяется длинной хорды, соединяющей…

Графическое изображение диаграммы направленности.

Представим ряд векторов, исходящих из одной точки по различным направлениям в пространстве, соответствующим различным значениям углов и , и имеющих… Изображение трехмерной диаграммы направленности по такому способу чрезвычайно… (2.14)

Двойной физический смысл пространственных частот.

, (2.16) . (2.17) Переменные и являются координатами точек пространства и имеют размерность длины. Переменные и имеют размерность,…

Фильтрующие свойства свободного пространства

  Рассмотрим сначала функцию, являющуюся двухмерной частотной характеристикой… .

ГРАНИЦА РАЗДЕЛА КАК ЭЛЕМЕНТ ИНФОРМАЦИОННОЙ СИСТЕМЫ

3.1 Частотная характеристика границы раздела

 

Для достаточно больших углов падения светового пучка на плоскую границу раздела не удаётся получить связь между исходным распределением поля источника и его эквивалентным распределением источника в отсутствии границы раздела в явном виде для произвольной функции распределения комплексной амплитуды. В этом случае частотный спектр изображения получится в случае линейных систем в виде произведения спектра пространственных частот G(ω) функции распределения комплексной амплитуды поля объекта M(x) на частотную характеристику передающей системы. В общем случае следует учитывать ограниченность частотной характеристики свободного пространства, однако в пароксимальном рассмотрении это заведомо излишне, так как область рассматриваемых частот ω < k .

G^'( ω) = W(ω)G(ω) , (3.1)

где G(ω), G'(ω) – спектры пространственных частот исходного и преобразованного поля соответственно. Следует отметить, что данное соотношение справедливо для линейных цепей, к которым нет основания причислять границу раздела (даже плоскую) в случае наклонного падения света. Действительно, связь между углом падения и преломления заведомо не линейна. Таким образом, если для нормального падения светового пучка частоты исходного и преобразованного полей совпадают, а преобразование спектра сводится к его линейной фильтрации, обусловленной существованием угловой зависимости пропускания границы раздела, то при наклонном падении светового пучка на границу раздела поворот плоскости локализации объекта, заданный в виде смещения в области пространственных частот на постоянную величину, не позволяет получить приближения удобные для анализа, а частоты исходного и преобразованного полей оказываются связанными не линейно. В связи со сказанным интерес представляет рассмотрение координатного преобразования осуществляемого границей раздела в спектральной области.

Пусть излучающий объект распложен в плоскости P(x₁) в среде с показателем U₁ (рисунок 11). Пусть также U₁(х₁) и U₂(х₂) – соответственно распределение комплексной амплитуды поля объекта и эквивалентного ему источника в отсутствии границы раздела, а

U₁( х₁) ↔ G₁(ω₁)

U₂( х₂) ↔ G₂(ω₂) (3.2)

- трансформанты Фурье,

где

 

 

 

Рисунок 11. Падение волны на плоскую границу раздела.

 

ω₁ = k₁ sin φ₁

ω₂ = k₂ sin φ₂ (3.3)

Тогда из закона Снеллиуса вытекает:

 

k₁sin(θ₁+φ₁) = k₂sin(θ₂+φ₂) (3.4)

или с учётом (3.3), после некоторых элементарных преобразований получим:

.(3.5)

Для больших углов падения и преломления в мало угловом приближении, то есть при

(3.6)

связь между частотами исходного и преобразованного полей представляется в виде:

,

откуда можно записать

(3.7)

 

При , дробь, в подкоренном выражении, удовлетворяет соотношению малости по сравнению с единицей и, разлагая корень в ряд по малости указанного выражения, для связи пространственных частот получим:

, (3.8)

 

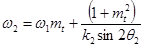, (3.9)

 

где .

Преобразование координат с точностью до квадратичных по отношениюмножителей оказывается взаимным. Таким образом, преобразование координат в спектре во втором приближении оказывается нелинейным и граница раздела не может быть рассмотрена в виде общего случая, в качестве элемента линейной цепи, а связь между спектрами исходного и преобразованного полей может быть представлена в виде:

. (3.10)

Таким образом, в частотной области спектр при преломлении из оптически более плотной в оптически менее плотную среду оказывается “растянут” и квадратично деформирован, что в действительности наблюдается на эксперименте, формально данное преобразование спектра может быть рассмотрено в виде интервала свёртки с δ-функцией Дирака:

. (3.11)

Где А(ω)- некоторая функция, определяющая изменение амплитуды поля вследствие неоднородного изменения масштаба в спектральной области. Вследствие закона сохранения можно записать для элементарного интервала пространственных частот ∆ω:

Ι(ω₁)∆ω₁=І(ω₂)∆ω₂

откуда

. (3.12)

Если учесть пропускание границы раздела, как функцию угла падения, то из формулы Френеля следует, для волны, поляризованной перпендикулярно плоскости падения:

. (3.13)

Из выражения следует, что производя учёт соотношений, можно получить зависимость пропускания границы раздела, как функцию частоты для малых φ₁ и φ₂:

. (3.14)

При построении плоского эквивалентного источника следует также учесть, что фазовый сдвиг обусловленный тем, что в лучевом приближении для преобразованного источника лучи не пересекаются в одной точке. Данное обстоятельство можно трактовать как сдвиг начала отсчёта в координатной плоскости эквивалентного источника для каждой гармоники на величину являющуюся функцией пространственной частоты. Приведение всех компонентов спектра пространственных частот к единой системе отсчёта можно осуществить путём введения фазового множителя:

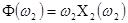. (3.15)

Из геометрических соображений (рис.) для величины сдвига можно получить выражение:

(3.16)

из выражения видно, что при использовании условия малости φ₁ и φ₂, а также использовании выражений (3.3) и (3.8) получаем:

, (3.17)

а положение эквивалентного источника определиться в виде:

. (3.18)

Таким образом, для связи спектров исходного и преобразованного полей можно записать, с учётом (3.10), (3.12), (3.13) и (3.17) с точностью до несущественного здесь частотного множителя

(3.19)

Данное выражение позволяет выделить следующие основные изменения в спектре при прохождении через границу раздела под углом, близким к углу полного внутреннего отражения наличие амплитудно-частотной характеристики, квадратичной по пространственной частоте, и, наконец, неоднородного преобразования координат в пространственно-частотной области.

 

 

Трансформация диаграммы направленности при переходе через границу раздела

 

 

Подставив в формулу (3.19) получим выражение, характеризующее трансформацию диаграммы направленности на плоской границе раздела:

 

Учитывая, что рассматриваются малые углы дифракции получим следующее выражение:

 

 

Проанализировав последнее выражение, приходим к выводу, что при переходе из оптически менее плотной в оптически более плотную среду с диаграммой направленности происходят следующие изменения:

 

- происходит сжатие (расширение) ширины главного лепестка;

 

 

 

 

 

 

- происходит квадратичный сдвиг, то есть “сдвигается” энергетический центр;

 

 

 

 

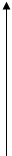
- наблюдается неравномерное ослабление:

 

 

Частотная характеристика границы раздела при квазинормальном падении

Теория цепей является мощным механизмом для определения параметров прохождения сигналов через сложные системы. В этой главе получено выражение для частотной характеристики границы раздела двух сред при квазинормальном падении.

Пусть излучающий объект расположен в плоскости в среде с показателем и , - соответственно распределение комплексной амплитуды поля объекта и эквивалентного ему источника в отсутствии границы раздела, а , 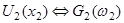- трансформанты Фурье, где

,

.

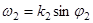Тогда из закона Снеллиуса вытекает

.

После некоторых элементарных преобразований можно получить выражение, определяющее связь между частотами исходного и преобразованного полей:

,

.

Преобразование координат с точностью до квадратичных по отношению множителей оказывается взаимным и нелинейным.

Рассмотрим выражение для частотной характеристики границы раздела, представленное в виде

.

 

Связь между спектрами исходного и преобразованного полей может быть рассмотрена в виде свертки с -функцией Дирака:

.

Пренебрегая зависимостью коэффициента ослабления от угла падения, что справедливо для применяемых приближений, следует учесть фазовую и амплитудную характеристики границы раздела:

,

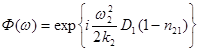где D₁ – расстояние от антенны до границы раздела, а

 

.

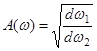В итоге получаем выражение, показывающее связь между спектрами исходного и преобразованного полей

.

 

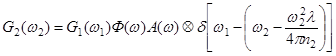3.4 Импульсный отклик границы раздела

 

 

При анализе прохождения сигнала через информационные системы перспективным представляется применение теории линейных цепей, основанной на понятиях частотной характеристики и импульсного отклика системы. Преобразование сигнала описывается, как свёртка исходного сигнала с импульсным откликом системы

,

где 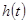- реакция системы на импульсное воздействие, то есть

,

если .

Данный подход имеет свои особенности применительно к радиотехническим системам. Рассмотрение процесса прохождения информационной волны через плоскую границу раздела двух непоглащающих изотропных сред можно провести в пространственно-частотном представлении, где каждой пространственной частоте преобразуемого поля соответствует определенный угол дифракции в разложении по плоским волнам. Тогда для малых углов дифракции частотная характеристика границы может быть представлена в виде:

,

где

,

Применим к соотношению характеризующему связь между преобразованным и исходным спектром преобразование Фурье:

.

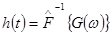Так как входной сигнал является δ-функцией, импульсный отклик можно рассматривать как Фурье-преобразование от спектра сигнала на выходе.

С учетом фазового множителя и преобразования координат связь исходного и преобразованного спектра можно выразить следующим образом:

.

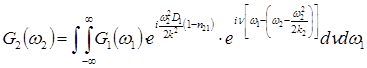Выражая спектр поля 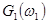через исходный сигнал ,

,

приходим к окончательному виду

.

 

Применим к спектру преобразованных частот преобразование Фурье:

 

.

Проинтегрировав последнее выражение по переменным и , получим

.

 

Произведем замену

,

,

получим

.

Так как,то

.

Окончательно приходим к выражению, характеризующему связь преобразованного и исходного сигналов

.

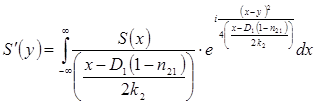Полагая, что , то можно получить реакцию границы раздела на импульсное воздействие, то есть – закон преобразования поля точечного источника (сферического излучателя) на плоской границе раздела двух сред:

.

Так как , то получим с точностью до несущественного здесь множителя:

.

Данное выражение является импульсным откликом границы раздела двух сред, то есль характеризует поле изотропного излучателя во второй среде.

 

 

Перечень ключевых слов: диаграмма направленности, импульсный отклик, частотная характеристика, преобразование Фурье.

В настоящей дипломной работе по литературным источникам было изучено спектральное представление сигналов, представление отклика линейной цепи в форме интеграла наложения, прохождение сигналов через линейные системы, частотная характеристика и импульсный отклик системы.

Решены задачи о пространственно-частотной характеристики границы раздела двух сред, об импульсном отклике границы раздела двух сред и о трансформации диаграммы направленности излучателя с произвольным распределением поля в раскрыве при дифракции на плоской границе раздела.

В работе рассмотрен процесс прохождения информационной волны через плоскую границу раздела в пространственно-частотном представлении.

 

 

СОДЕРЖАНИЕ

 

СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ

1.2 Преобразование Фурье 1.3 Понятие спектральной плотности сигнала 1.4 Обратное преобразование Фурье

ДИАГРАММА НАПРАВЛЕННОСТИ ИЗЛУЧАЮЩЕЙ СИСТЕМЫ

2.2 Графическое изображение диаграммы направленности 2.3 Двойной физический смысл пространственных частот 2.4 Фильтрующие свойства свободного пространства