Плотность вероятности функции от случайной величины.

Пусть Y — случайная величина, связанная с X однозначной функциональной зависимостью вида у = f(x). Попадание случайной точки х в интервал шириной dx и попадание случайной точки у в отвечающий ему интервал шириной |dy| = |f'(х)|dx являются эквивалентными событиями, поэтому вероятности их совпадают:

p_x(x)dx = p_y(y) |dy|.

Отсюда

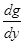Р_y (y) = Р_x(х) || = P_x[g (у)]|| , (6.11) ,

где х = g (у) — функция, обратная по отношению к у =f(x). Если функциональная связь между X и Y неоднозначна, так что имеется несколько обратных функций x₁=g₁(y), x₂ =g₂(y), …,x_n =g_N(y), то формула (6.11) обобщается следующим образом:

 

Р_у(у)= (6.12)

 

Характеристическая функция.

 

В теории вероятностей большую роль играет статистическое среднее вида

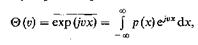(6.13)

называемое характеристической функцией случайной величины X. С точностью до коэффициента функции Θ(υ) есть преобразование Фурье от плотности вероятности, поэтому

(6.14)

Опуская элементарные выкладки, приведем некоторые результаты:

для случайной величины, равномерно распределенной на отрезке a ≥ х ≥ 0,

 

(6.15)

 

для гауссовой случайной величины с заданными параметрами т,

 

(6.16)

 

Располагая характеристической функцией, легко найти моменты случайной величины. Действительно, так как

 

 

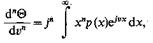
то, полагая здесь υ = 0 и сравнивая результат с (6.3), находим

 

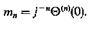(6.17) .

 

С помощью характеристической функции удобно также находить плотность вероятности случайной величины, подвергнутой функциональному преобразованию.

 

Статистические характеристики систем случайных величин

 

Свойства случайных сигналов принято описывать, рассматривая не просто те величины, которые наблюдаются в какой-нибудь момент времени, а изучая совокупности этих величин, относящихся к различным фиксированным моментам времени.