Функция распределения и плотность вероятности.

Пусть даны случайные величины {Х₁ Х₂,…,Х_n}, образующие n-мерный случайный вектор X. По аналогии, с одномерным случаем функция распределения этого вектора

 

Отвечающая ей n-мерная плотность вероятности p(x₁, х₂,…, х_n) удовлетворяет соотношению

 

 

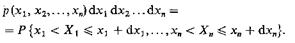
Очевидно, функция распределения может быть найдена путем интегрирования плотности вероятности:

 

 

Любая многомерная плотность обладает свойствами, обычными для плотности вероятности:

 

 

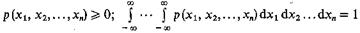
Зная n-мерную плотность, всегда можно найти n-мерную плотность при m <n, интегрируя по «лишним» координатам:

 

 

Вычисление моментов. Располагая соответствующей многомерной плотностью вероятности, можно находить средние значения любых комбинаций из рассматриваемых случайных величин и, в частности, вычислять их моменты. Так, ограничиваясь наиболее важным для дальнейшего случаем двумерной случайной величины, по аналогии с (6.4), (6.7) находим математические ожидания

 

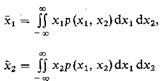(6.18) '

и дисперсии

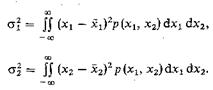(6.19)

Новой по сравнению с одномерным случаем является возможность образования смешанного момента второго порядка

(6.20)

называемого ковариационным моментом системы двух случайных величин.