Корреляция.

Предположим, что проведена серия опытов, в результате которых каждый раз наблюдалась двумерная случайная величина {Х₁ Х₂}. Условимся исход каждого опыта изображать точкой на декартовой плоскости.

Может оказаться, что изображающие точки в среднем располагаются вдоль некоторой прямой, так что в каждом отдельном испытании величины х₁ и х₂ имеют чаще всего одинаковый знак. Это наводит на мысль о том, что между х₁ и х₂ есть статистическая связь, называемая корреляцией.

Однако возможен случай хаотического расположения точек на плоскости. Говорят, что при этом рассматриваемые величины некоррелированы, т. е. между ними нет устойчивой связи в вероятностном смысле.

Количественной характеристикой степени статистической связи двух случайных величин служит их ковариационный момент К₁₂ или, что часто удобнее, корреляционный момент R₁₂, определяемый как среднее значение произведения

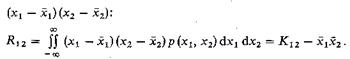
Вводят также безразмерный коэффициент корреляции r₁₂=K₁₂/(σ₁σ₂). (6.22)

Для совпадающих случайных величин, когда х₁ = х₂, имеют место равенства

R₁₁ = R₂₂ = σ² , r₁₁ = r₂₂ = 1

Если размерность случайного вектора больше двух, то можно построить всевозможные перекрестные корреляцион­ные моменты

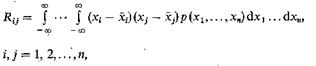
и коэффициенты корреляции которые объединяются в соответствующие матрицы

Можно показать, что всегда,|r_ij| ≤ 1, причем равенство возможно лишь при условии x_i = ±x_j (полностью коррелированные величины).

 

Статистическая независимость случайных величин.

По определению, случайные величины Х₁ Х₂,...,Х_n статистически независимы, если их многомерная плотность вероятности может быть представлена в виде произведения соответствующих одномерных плотностей:

 

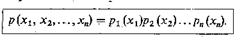(6.23)

 

Статистически независимые случайные величины некоррелированы между собой. Действительно, для них

 

 

при i ≠ j . Обратное утверждение в общем случае неверно: из некоррелированности не вытекает автоматически статистическая независимость случайных величин.