Передача информации от непрерывного источника.

Количество информации, получаемой от непрерывного источника по каналу с помехами, определяется так же, как в случае, рассмотренном выше, но с использованием понятия дифференциальной энтропии.

Для источника, имеющего непрерывное множество состояний, среднее количество информации, содержащееся в каждом принятом значении случайной величины W относительно переданного значения случайной величины Z, можно получить как разность априорной и апостериорной дифференциальных энтропии:

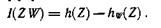
Соотношение несложно выразить в виде:

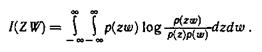
Относительность дифференциальных энтропий в этом случае не принимается во внимание, поскольку количество информации не зависит от выбранного стандарта сравнения.

Основные свойства количества информации. 1. Несмотря на то, что частное количество информации может быть величиной отрицательной, количество информации неотрицательно.

Действительно, согласно выражению

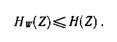
Тогда

2. При отсутствии статистической связи между случайными величинами Z и W

следовательно, в этом случае

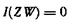
(принятые элементы сообщения не несут никакой информации относительно переданных).

3. Количество информации в W относительно Z равно количеству информации в Z относительно W.

Для доказательства этого утверждения воспользуемся выражением

 

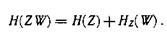
Аналогично можно записать

 

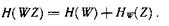
Так как H(ZW) = H(WZ), то

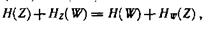
откуда

4. При взаимно однозначном соответствии между множествами передаваемых и принимаемых элементов сообщений, что имеет место в отсутствии помехи, апос­териорная энтропия равна нулю и количество информа­ции численно совпадает с энтропией источника:

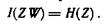
Это максимальное количество информации о состоянии дискретного источника. Для непрерывного источника оно равно бесконечности.

 

ПОНЯТИЕ ИНФОРМАЦИОННОГО СИГНАЛА

 

В зависимости от структуры информационных параметров сигналы подразделяют на дискретные, непрерывные и дискретно-непрерывные.

Сигнал считают дискретным по данному параметру, если число значений, которое может принимать этот параметр, конечно (или счетно). Если множество возможных значений параметра образует континуум, то сигнал считают непрерывным по данному параметру. Сигнал, дискретный по одному параметру и непрерывный по другому, называют дискретно-непрерывным.

В соответствии с этим существуют следующие разновидности математических представлений (моделей) детерминированного сигнала:

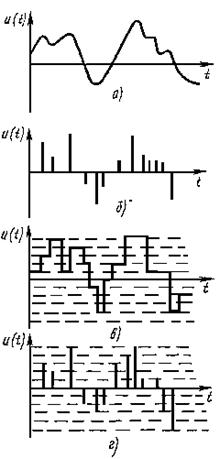непрерывная функция непрерывного аргумента, например непрерывная функция времени (рис.3,а);

непрерывная функция-дискретного аргумента, например функция, значения которой отсчитывают только в определенные моменты времени (рис. 3,6)

дискретная функция непрерывного аргумента, например функция времени, квантованная по уровню (рис. 3, в);

дискретная функция дискретного аргумента, например функция, принимающая одно из конечного множества возможных значений (уровней) в определенные моменты времени (рис. 3, г).

Рассматриваемые модели сигналов в виде функций времени предназначены в первую очередь для анализа формы сигналов. Желательно найти такое представление сигнала, которое облегчает задачи исследования прохождения реальных сигналов, часто имеющих достаточно сложную форму, через интересующие нас системы. С этой целью сложные сигналы представляются совокупностью элементарных (базисных) функций, удобных для последующего анализа.

Наиболее широкий класс исследуемых систем — это инвариантные во времени линейные системы.

При анализе прохождения сложного сигнала u{t) через такие системы его представляют в виде взвешенной суммы базисных функций j_k(t) (или соответствующего ей интеграла):

(1.1)

где [t₁, t₂] —интервал существования сигнала.

При выбранном наборе базисных функций сигнал u(t) полностью определяется совокупностью безразмерных коэффициентов С_k. Такие совокупности чисел называют дискретными спектрами сигналов.

На интервале [t₁, t₂] выражение (1.1) справедливо как для сигналов, неограниченных во времени, так и для сигналов конечной длительности. Однако за пределами интервала сигнал конечной длительности не равен нулю, так как он представляется суммой в том случае, если условно считается периодически продолжающимся. Поэтому, когда для ограниченного во времени сигнала необходимо получить представление, справедливое для любого момента времени, используется интеграл:

(1.2)

где j(a, t) — базисная функция с непрерывно изменяющимся параметром а.

В этом случае имеется непрерывный (сплошной) спектр сигнала, который представляется спектральной плотностью S(a). Размерность ее обратна размерности a. Аналогом безразмерного коэффициента C_k здесь является величина S(a)da.

Совокупность методов представления сигналов в виде (1.1) и (1.2) называют обобщенной спектральной теорией сигналов. В рамках линейной теории спектры являются удобной аналитической формой представления сигналов.

Для теоретического анализа базисные функции j_k(t) нужно выбирать так, чтобы они имели простое аналитическое выражение, обеспечивали быструю сходимость ряда (1.1) для любых сигналов u(t) и позволяли легко вычислять значения коэффициентов C_k. Базисные функции не обязательно должны быть действительными, их число может быть неограниченным (-¥ ³ k ³ ¥).

В случае практической аппроксимации реального сигнала совокупностью базисных сигналов решающее значение приобретает простота их технической реализации. Сигнал представляется суммой ограниченного числа действительных линейно независимых базисных функций (сигналов).

Ортогональные представления сигналов. Вычисление спектральных составляющих сигнала существенно облегчается при выборе в качестве базиса системы ортогональных функций.

Систему функций y₀(t),y₁(t),…,y_n(t)называют ортогональной на отрезке [t_a, t_b], если для всех k , за исключением случая k = j, удовлетворяется условие

(1.3)

Эта система функций будет ортонормированной (ортонормальной), если для всех j справедливо соотношение

(1.4)

Если соотношение (1.4) не выполняется и

 

 

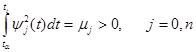
то систему можно нормировать, умножая функции y_j(t)на 1/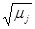

Определим коэффициенты C_k при представлении сигнала u(t) совокупностью ортонормированных функций в виде

 

(1.5)

предполагая, что интервал [t₁, t₂] лежит внутри отрезка ортогональности [t_a, t_b].

Правую и левую части уравнения (1.5) умножаем на y_j(t) и интегрируем на интервале [t₁, t₂] :

 

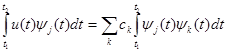(1.6)

В силу справедливости условия (1.3) все интегралы в правой части выражения (1.6) при k ¹j будут равны 0. При k = j в соответствии с (1.4) интеграл равен 1. Следовательно,

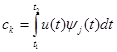(1.7)

В теоретических исследованиях обычно используют полные системы ортогональных функций, обеспечиваю­щие сколь угодно малую разность непрерывной функции u(t) и представляющего ее ряда при неограниченном увеличении числа его членов. Разность оценивают по критерию

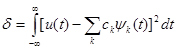(1.8)

При этом говорят о среднеквадратической сходимости ряда 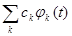к функции u(t). Широко известной ортонормированной системой является совокупность тригонометрических функций, кратных аргументов.Она ортонормальна

 

 

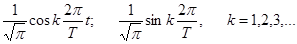
на отрезке [-p, p]. Так как соответствующее разложение исторически появилось первым

и было названо рядом Фурье, то соотношение (1.5) часто именуют обобщенным рядом Фурье, а значения C_k — обобщенными коэффициентами Фурье.

Известны представления сигналов по системам ортогональных базисных многочленов Ко-тельникова, Чебышева, Лаггера, Лежандра и др., а также неортогональные разложения по функциям Лагранжа,Тейлора и др.

Обощенная спектральная теория облегчает решение проблемы обоснованного выбора базисных функций для конкретных задач анализа процессов, происходящих при формировании и прохождении сигналов через те или иные звенья информационной системы.

 

ВРЕМЕННАЯ ФОРМА ПРЕДСТАВЛЕНИЯ СИГНАЛА

 

Временным представлением сигнала называют такое разложение сигнала u(t), при котором в качестве базис­ных функций используются единичные импульсные функ­ции — дельта-функции. Математическое описание такой функции задается соотношениями

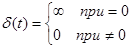(1.9)

 

 

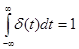
где d(t)— дельта-функция, отличная от нуля в начале координат (при t = 0).

Для более общего случая, когда дельта-функция отличается от нуля в момент времени t = x₁ (рис.),

имеем

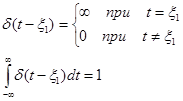(1.10)

 

Такая математическая модель соответствует абстрактному импульсу бесконечно малой длительности и безграничной величины. Единственным параметром, правильно отражающим реальный сигнал, является время его действия. Однако, учитывая (1.10), с помощью дельта-функции можно выразить значение реального сигнала u(t) в конкретный момент времени x₁:

(1.11)

Равенство (1.11) справедливо для любого текущего момента времени t. Заменив £i на t и приняв в качестве переменной интегрирования |, получим

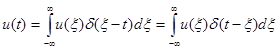(1.12)

Таким образом, функция u(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Ортогональность совокупности таких импульсов очевидна, так как они не перекрываются во времени.

Разложение (1.12) имеет большое значение в теории линейных систем, поскольку, установив реакцию системы на элементарный входной сигнал в виде дельта-функции (импульсную переходную функцию), можно легко определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с «площадями», равными соответствующим значениям входного сигнала.

С помощью дельта-функций можно также представить периодическую последовательность идеализированных импульсов с постоянными или меняющимися уровнями. Обозначив через u_n(t) функцию, равную u(kDt) в точках t = kDt и нулю в остальных точках, запишем:

 

 

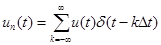
где Dt — период следования импульсов.

Поскольку умножение u{t) на дельта-функцию в момент времени t = kDt соответствует получению отсчета этой функции, u_n(kAt) может представлять результат равномерной дискретизации функции u(t).

Дельта-функцию d(x) в точке x = 0 можно рассматривать как предел множества действительных непрерывных функций, подобных функциям Гаусса:

 

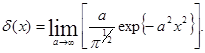
(2.2)

 

 

При этом вместе с величиной а максимальное значение функции Гаусса стремится к бесконечности, полуширина (1/а) стремится к нулю, в то время как интеграл этой функции всегда равен едини­це. Отсюда следует, что дельта-пункция удобна для описания лю­бой функции, имеющей форму пика с пренебрежимо (в эксперименте) малой полушириной.

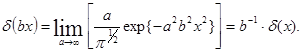Подобным же образом дельта-функция с∙d(х) используется для описания резкого пика, интеграл которого равен с. Для более ясного понимания или

 

доказательства различных соотношений удобно определять дельта-функцию как предел ряда функций.

Можно определить дельта-функцию в двух измерениях d(х, у), которая равна нулю всюду, кроме точки х = у = 0, и для которой:

 

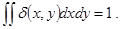
Подобным же образом можно определить дельта-функцию для любого числа измерений d(r) или d(r—a), где r и а — векторы n-мерного пространства.

Заметим, что в двух измерениях d(х) является линией, а в трех измерениях — плоскостью.

Отметим другое важное определение дельта-функции:

 

(2.3)

 

которое встретится позже в связи с рассмотрением фурье-преобра-зований.