Ряды Фурье.
Зададим на интервале времени [-T/2, T/2] ортонормированный базис, образованный гармоническими функциями с кратными частотами:
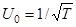 ,
,
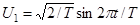 ,
,
 , (1.2)
, (1.2)
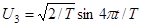 ,
,
 , …
, …
Любая функция  принадлежащая этому базису, удовлетворяет условию периодичности (1.1). Выполнив разложение сигнала
принадлежащая этому базису, удовлетворяет условию периодичности (1.1). Выполнив разложение сигнала  в этом базисе, т. е. вычислив коэффициенты
в этом базисе, т. е. вычислив коэффициенты
 , (1.3)
, (1.3)
получаем его спектральное представление
 . (1.4)
. (1.4)
Разложение справедливо на всей вертикальной оси времени. Ряд вида (1.4) называется рядом Фурье.
Введем основную частоту 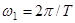 последовательности, образующий периодический сигнал. Вычисляя коэффициенты разложения по формуле (1.3), ряд Фурье для периодического сигнала имеет вид:
последовательности, образующий периодический сигнал. Вычисляя коэффициенты разложения по формуле (1.3), ряд Фурье для периодического сигнала имеет вид:
 , (1.5)
, (1.5)
где  - среднее значение за период, или постоянная составляющая сигнала;
- среднее значение за период, или постоянная составляющая сигнала;  - соответственно амплитуды косинусоидальных и синусоидальных составляющих:
- соответственно амплитуды косинусоидальных и синусоидальных составляющих:
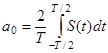 ,
,
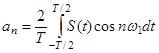 , (1.6)
, (1.6)
 .
.
В общем случае периодический сигнал содержит в себе не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами 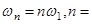 1,2,3, … , кратными основной частоте последовательности (рис. 1).
1,2,3, … , кратными основной частоте последовательности (рис. 1).






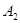
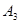



 |


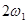
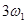 …
… 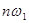
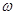
Рисунок 1. Амплитудный спектр периодического сигнала.
Любая гармоника ряда Фурье характеризуется амплитудой 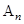 и начальной фазой
и начальной фазой 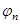 . Для этого коэффициенты ряда следует записывать в виде
. Для этого коэффициенты ряда следует записывать в виде
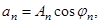

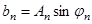 ,
,
так что
 ;
;
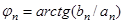 .
.
Подставив эти выражения в (1.5), получим другую, эквивалентную формулу ряда Фурье
 , (1.7)
, (1.7)
которая иногда оказывается удобнее.
Ряд Фурье в комплексной форме имеет следующий вид:
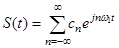 , (1.8)
, (1.8)
где 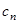 - коэффициент ряда Фурье
- коэффициент ряда Фурье
 . (1.9)
. (1.9)