Свертки
В одном измерении интеграл свертки двух функций f(х)и g(х) определяется как:
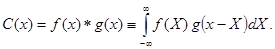
(2.4)
Путем простой замены переменных находим:
(2.5)
Для двух или более измерений можно воспользоваться векторной формой:
(2.6)
Тождественной операцией является свертка с дельта-функцией Дирака:
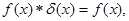
(2.7)
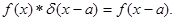
Пример свертки дает принцип Гюйгенса, записанный в виде формул Кирхгофа. Каждая точка фронта волны рассматривается как источник сферической волны, начальная амплитуда которой пропорциональна амплитуде падающей волны, Затем амплитуды вторичных волн складываются и дают амплитуду в плоскости наблюдения. Таким образом, функция амплитуды g(x, у) на начальном фронте волны рассеивается с помощью функции, которая представляет вторичную сферическую волну от точечного источника на фронте волны.
Для дифракции Френеля в малоугловом приближении записать:
(2.10)
Функцию в квадратных скобках можно назвать функцией распространения, или волновой функцией точечного источника, q(х, у) =d(х, у).
ЧАСТОТНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ СИГНАЛА
Любой физически реализуемый сигнал ограничен во времени и обладает конечной энергией. Функции, отображающие реальные сигналы, удовлетворяют условиям Дирихле и абсолютно интегрируемы, т. е.
(1.40)
где М — конечная величина.
Модели таких сигналов также могут быть представлены совокупностью гармонических составляющих в соответствии с выражением (1.2). Конкретный вид спектрального преобразования для непериодического сигнала получим, проследив изменения, происходящие в спектре периодической последовательности импульсов ii(f) при увеличении периода их повторения.
Пару преобразований Фурье для периодической функции u1(t) запишем в форме (1.15) и (1.16):
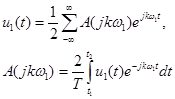
При Т® ¥ u1(t) переходит в u(t), частота w1 уменьшается до dw, a kw1 превращается в текущую частоту w. Заменяя суммирование интегрированием, находим
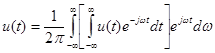
Обозначив интеграл в квадратных скобках S(jw), получим формулы для прямого и обратного интегрального преобразования Фурье:
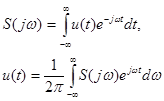(1.41-1.42)
Величину S(jw) называют комплексной спектральной плотностью или спектральной характеристикой. Она имеет размерность [амплитуда/частота]. На каждой конкретнойчастоте амплитуда соответствующей составляющей равна нулю. Сравнивая (1.15) и (1.42), находим, что бесконечно малому интервалу частоты dw соответствует составляющая с бесконечно малой комплексной амплитудой dA(jw):
(1,43)
Сравнение выражения (1.41) для спектральной характеристики функции u(t), с формулой (1.17) для огибающей комплексного спектра такой же функции, периодически продолжающейся во времени, показывает, что они различаются только множителем:
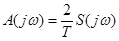(1.44)
Поэтому по известной спектральной характеристике одиночного импульса легко построить линейчатый спектр их периодической последовательности. Соотношением (1.44) объясняется и тот факт, что для различных представлений спектральной характеристики имеют место формулы, весьма похожие на (1.18) — (1.24).
Как комплексная величина спектральная характеристика может быть записана в виде
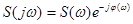(1.45)
где S(w) = |S(jw)| называется спектральной плотностью амплитуд или спектром непериодического сигнала.
Так как составляющие расположены на всех частотах, то спектр непериодического сигнала является непрерывным или сплошным. Представим спектральную характеристику состоящей из действительной и мнимой частей:
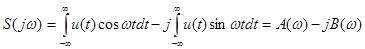(1.46)
где
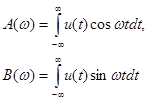(1.47 - 1-48)
Модуль спектральной характеристики S(w) определяется выражением
(1.49)
и представляет собой четную функцию частоты.
Для фазы спектральной характеристики S(w) соответственно получаем
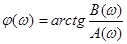(1.50)
Так как из (1.42) и (1.43) следует, что A(w) — четная функция частоты, а В(w) — нечетная, то функция j(w) относительно частоты нечетна.
Комплексная форма интегрального преобразования Фурье легко приводится к тригонометрической:
Второй член в связи с нечетностью подынтегрального выражения равен нулю. Окончательно имеем
(1.51)
Преимущество тригонометрической формы записи Фурье-преобразования заключается в возможности некоторого физического толкования с использованием идеализации, не очень далеких от реальности.