Импульсные, переходные и частотные характеристики линейных систем.
Замечательная особенность линейных систем – справедливость принципа суперпозиции – открывает прямой путь к систематическому решению задач о прохождении разнообразных сигналов через такие системы. Способ динамического представления позволяет представить сигналы в виде сумм элементарных импульсов. Если удаётся тем или иным способом найти реакцию на выходе, возникающую под действием элементарного импульса на входе, то окончательным этапом решения задачи явится суммирование таких реакций.
Такой анализ основан на временном представлении свойств сигналов и систем. В равной мере применим, а порой и гораздо более удобен анализ в частотной области, когда сигналы задаются рядами или интегралами Фурье. Свойства систем при этом описываются их частотными характеристиками, которые указывают закон преобразования элементарных гармонических сигналов.
Импульсной характеристикой системы называется функция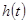 
, являющаяся откликом системы на входной сигнал 
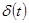. Это означает, что функция 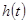удовлетворяет уравнению
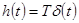. (1.41)
Поскольку система стационарна, аналогичное уравнение будет и в случае, если входное воздействие смещено во времени на производную величину t0 :
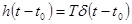. (1.42)
Импульсная характеристика, так же как и порождающая её дельта-функция, есть результат разумной идеализации. С физической точки зрения импульсная характеристика приближённо отображает реакцию системы на входной импульсный сигнал произвольной формы с единичной площадью при условии, что длительность этого сигнала пренебрежимо мала по сравнению с характерным временным масштабом системы, например периодом её собственных колебаний.
Зная импульсную характеристику линейной стационарной системы, можно формально решить любую задачу о прохождении сигнала через такую систему. Входной сигнал допускает представление вида
.
Отвечающая ему выходная реакция
. (1.43)
Интеграл – это предельное значение суммы , поэтому линейный оператор T на основании принципа суперпозиции может быть внесен под знак интеграла. Далее, оператор Т “действует” лишь на величины, зависящие от текущего времени 
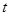, но не от переменной интегрирования 
. Поэтому из выражения (1.43) следует, что
. (1.44)
Эта формула называется интегралом Дюамеля и свидетельствует о том, что выходной сигнал линейной стационарной системы представляет собой свёртку двух функций – входного сигнала и импульсной характеристики системы.
Каков бы ни был конкретный вид импульсной характеристики, всегда должен выполняться важнейший принцип: выходной сигнал, отвечающий импульсному входному воздействию, не может возникнуть до появления импульса на входе.
Отсюда вытекает очень простое ограничение на вид допустимых импульсных характеристик:
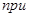
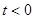. (1.45)
Для физически реализуемой системы верхний предел в формуле интеграла Дюамеля может быть заменён на текущее значение времени:
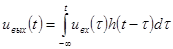. (1.46)
Физически реализуемая система должна быть устойчивой. Это означает, что её импульсная характеристика должна удовлетворять условию абсолютной интегрируемости
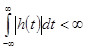. (1.47)
Пусть на входе линейной стационарной системы действует сигнал, изображаемый функцией Хевисайда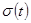 
. Выходную реакцию
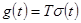(1.48)
принято называть переходной характеристикой системы. Поскольку система стационарна, переходная характеристика инвариантна относительно временного сдвига:
.
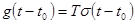Между импульсной и переходной характеристикой имеется тесная связь. Действительно, так как
,
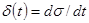то на основании (1.41)
.
Оператор дифференцирования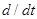 
и линейный стационарный оператор T могут меняться местами, поэтому
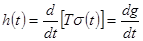, (1.49)
или
. (1.50 )
Функция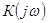 
- частотный коэффициент передачи между j-м входом и i-м выходом. Она имеет простую интерпретацию: если на вход системы поступает гармонический сигнал с известной частотой 
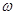и комплексной амплитудой 
, то комплексная амплитуда выходного сигнала
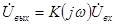. (1.51)
Часто пользуются представлением частотного коэффициента передачи в показательной форме:
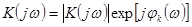. (1.52)
Обе входящие сюда вещественные функции носят специальныеназвания: 
- амплитудно-частотная характеристика (АЧХ), 
- фазочастотная характеристика (ФЧХ) системы.
1.11 Частотная характеристика и импульсный отклик свободного пространства.
Как колебательные так и волновые процессы описываются линейными дифференциальными уравнениями и совершаются в так называемых “линейных системах”. Для того чтобы система была линейной, необходимо, чтобы выполнялся так называемый принцип суперпозиции, который состоит в следующем: если входное воздействие представлено в виде некоторой суммы воздействий x1+x2+…+xn ,то и выходной сигнал системы должен быть представлен в виде суммы выходных сигналов y1+y2+…+yn таких , что каждое слагаемое yi является результатом воздействия на систему соответствующего слагаемого xi , действующего независимо от других. Кроме принципа суперпозиции необходимо выполнение ещё одного принципа – принципа транспозиции. Принцип транспозиции состоит в том, что форма выходного сигнала не зависит от момента начала входного воздействия и он смещается во времени на такой же интервал, на который смещается момент начала входного сигнала.
На основании этих двух свойств можно реакцию (называемую также откликом) линейной системы на какое-либо входное воздействие представить в виде суммы реакций на какие-либо более простые входные воздействия.
В радиотехнике употребительны два типа входных воздействий, по реакциям на которые обычно разлагаются реакции на любое произвольное воздействие. Это функция вида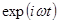 
и 
функция. Реакция линейной системы на входное воздействие вида 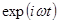называется частотной характеристиской системы 
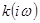, а реакция на функцию 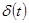называется импульсной характеристикой 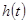. C помощью этих характеристик реакция линейной системы 
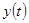на некоторое входное воздействие 
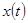выражается следующим образом:
, (1.53)
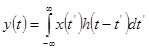, (1.54)
где Cx(ω) - спектр входного воздействия, определяемый выражением
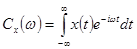, (1.55)
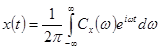. (1.56)
Соотношение (1.53) является простым следствием принципов суперпозиции, транспозиции и соотношения (1.56). В самом деле, соотношение (1.56) представляет входной сигнал в виде суммы воздействий вида 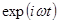с амплитудами и фазами, определяемыми комплексным множителем Cx(ω). На каждое слагаемое exp(iωt) во входном воздействии следует отклик вида 
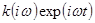. Изменение амплитуды и фазы входного воздействия 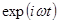, описываемое множителем 
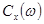, должно, согласно принципу транспозиции, передаваться на выходной сигнал в виде таких же изменений.
В результате суммирования выходных сигналов, являющихся откликами на члены суммы (1.56) получается выражение (1.53).
Выражение (1.54) получается при применении принципов суперпозиции и транспозиции к входному сигналу, записываемому в виде следующей суммы
.
В выходном сигнале каждая δ-функция входного воздействия заменяется на h(t) . При этом согласно принципу транспозиции аргументом этой функции служит аргумент δ-функции. Если в качестве входного воздействия x(t) взять δ(t), то из (1.53) мы получим связь между импульсной и частотной характеристиками в виде
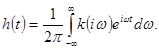(1.57)
Обращая этот интеграл Фурье, получаем
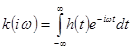. (1.58)
Рассмотрим следующее выражение
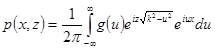(1.59)
и сравним его с выражением (1.53).
Эти выражения имеют аналогичный вид. Функция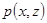 
представляет собой комплексную амплитуду поля, прошедшего путь z в свободном пространстве. Естественно считать её откликом свободного пространства на входной сигнал, действующий в начале этого участка при 
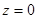. Под знаком интеграла (1.59) стоит функция 
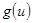, которая аналогично 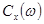является спектром входного сигнала. Переменную интегрирования 
, являющуюся аргументом в разложении в интеграл Фурье входного пространственного распределения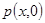
, назовём пространственной частотой. Наконец функция
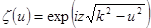
является аналогом функции 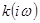- частотной характеристики линейной системы.
Таким образом, запись решения волнового уравнения в форме (1.59) позволяет установить основные характеристики свободного пространства как линейной системы.
Для более удобного рассмотрения введённых аналогий обратимся к рисунку 5, где изображены эквивалентные схемы линейного четырехполюсника и свободного пространства.
Входным сигналом линейного четырехполюсника, изображённого на рисунке 5,а, является функция времени 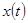. Линейный четырехполюсник имеет частотную характеристику 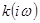и импульсную характеристику .
|
|
 |  |  |  |
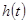