Фильтрующие свойства свободного пространства

 

 

Рассмотрим сначала функцию, являющуюся двухмерной частотной характеристикой свободного пространства:

.

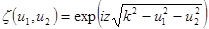Если изобразить на плоскости , то получится картина, показанная на рисунке 9.

 

 

 

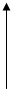
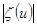
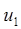
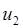
Рисунок 9. Модуль частотной характеристики свободного пространства на плоскости пространственных частот.

 

 

 

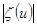
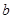
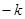
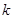
Рисунок 10. Модуль частотной характеристики свободного пространства как функция абсолютного значения пространственной частоты.

 

На рисунке по вертикали отложены значения , а по осям горизонтальной плоскости – аргументы функции. Получающаяся картина напоминает спиленное дерево. Уклон ствола зависит от расстояния 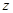и не одинаков для разных 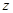. Это показано на рисунке 10, где дано сечение “пня” плоскостью, в которой лежит вертикальная ось. Для определённости выбрана плоскость, в которой расположена прямая . Кривая соответствует меньшему значению 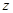, а кривая 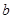- большему.

При увеличении 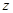форма приближается к прямоугольной форме. Представляет интерес оценить, при каких 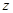её можно считать прямоугольной. Для этого потребуем, чтобы спад кривой в раз происходил на таком интервале 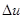, длина которого на много меньше интервала, где 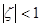. Условие спада в раз будет выглядеть следующим образом

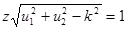. (2.19)

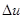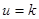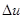Величину мы отсчитываем от . Учитывая осевую симметрию частотной характеристики, расчет сделаем для изменения только . На основании (2.19) для получаем

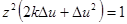. (2.20)

Эта величина 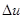должна быть много меньше 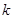, так как именно 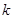определяет ширину интервала при 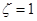. Поэтому в (2.20) можно пренебречь 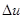по сравнению с 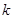и мы получим искомое выражение в виде

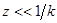(2.21)

или, что эквивалентно,

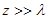. (2.22)

Таким образом, мы будем считать модуль частотной характеристики прямоугольным при выполнении условия (2.22), то есть на расстояниях 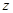, значительно превышающих длину волны.

Это рассмотрение показывает, что свободное пространство при 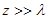представляет собой прямоугольный фильтр, который практически не пропускает частот со значениями . Фильтрация такого рода объясняет, что приближение Кирхгофа для описания поля на препятствии позволяет с приемлемой точностью решать дифракционные задачи. В самом деле, принимая, что поле на границе между прозрачными и непрозрачными частями объекта испытывает резкий скачок, мы совершаем заведомую ошибку. Однако пространственный спектр такого резкого скачка очень широкий. Вся ошибка при этом будет сосредоточена в той области пространственных частот, которая все равно будет отрезана свободным пространством. Если же взять только ту часть входного распределения поля, спектр, который попадает в область прозрачности свободного пространства, то мы получим совсем другое распределение с плавным переходом от прозрачного к непрозрачному, с медленным убыванием поля в области тени.

.