Соотношение между длительностью колебанияи шириной его спектра. Определения длительности колебания

При рассмотрении спектральной функции любого импульсного колебания можно установить, что чем сосредоточеннее, короче импульс во времени, тем протяженнее его спектральная функция по частоте, т. е. тем шире ее модуль. Это —общая закономерность, непосредственно вытекающая из теоремы об изменении масштаба времени колебания (§ 1.4). Спектральная функция удлиненного импульса

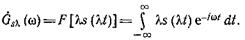
Вводя новую переменную интегрирования t^/= lt, получим

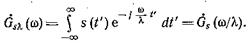
Функция l< 1 более сжата по сравнению с G_s(w). При сжатии импульса происходит обратное явление —расширение спектральной функции.

Понятие длительности (продолжительности) определено лишь для П-образного импульса и сходных с ним. Для других импульсов это понятие необходимо соответствующим образом ввести. Это же относится и к ширине спектра.

20---21---------------Функция распределения и плотность вероятности.

Пусть X — случайная величина, т. е. совокупность всевозможных вещественных чисел х, принимающих случайные значения. Исчерпывающее описание статистических свойств X можно получить, располагая неслучайной функцией F(x) вещественного аргумента х, которая равна вероятности того, что случайное число из X примет значение, равное или меньшее конкретного х:

Функция F(x) называется функцией распределения случайной величины X. Если X может принимать любые значения, то F(x) является гладкой неубывающей функцией, значения которой лежат на отрезке 1 ³ F(x) ³ 0. Имеют место следующие предельные равенства: F(-¥) = 0, F(¥) = 1.

Производная от функции распределения р(х) = dF/dx есть плотность распределения вероятности (или, короче, плотность вероятности) данной случайной величины. Очевидно, что

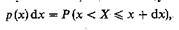
т. е. величина р(х)dx есть вероятность попадания случайной величины X в полуинтервал (х, х + dx).

Для непрерывной случайной величины X плотность вероятности р(х) представляет собой гладкую функцию. Если же X — дискретная случайная величина, принимающая фиксированные значения (х₁, х₂, … , х_n,...) с вероятностями (Р₁ Р₂, … , P_n,…) соответственно, то для нее плотность вероятности выражается как сумма дельта-функций:

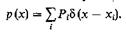
В обоих случаях плотность вероятности должна быть неотрицательной: р(х)>0 и удовлетворять условию нормировки

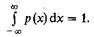
22----23---------------------Усреднение. Моменты случайной величины.

Результатами экспериментов над случайными величинами, как правило, служат средние значения тех или иных функций от этих величин. Если j(х) — известная функция от х (исхода случайного испытания), то, по определению, ее среднее значение

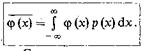
следует заметить следующее: наибольший вклад в среднее значение дают те участки оси х, где одновременно велики как усредняемая функция j(х), так и плотность вероятности р(х). В статистической радиотехнике широко применяются особые числовые характеристики случайных величин, называемые их моментами. Момент n-го порядка случайной величины X есть среднее значение n-й степени случайной переменной:

(6.3)

Простейшим является момент первого порядка, так называемое математическое ожидание

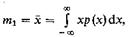(6.4)

которое служит теоретической оценкой среднего значения случайной величины, получаемого в достаточно обширных сериях испытаний. Момент второго порядка,

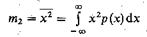(6.5)

является средним квадратом случайной величины.

Используются также центральные моменты случайных величин, задаваемые следующей общей формулой:

(6.6)

Важнейший центральный момент - так называемая дисперсия

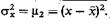
Очевидно, что

Величина s_х, т. е. квадратный корень из дисперсии, называется средним квадратическим отклонением, которое служит для количественного описания меры разброса результатов отдельных случайных испытаний относительно математического ожидания.