Функции Лагранжа

Исторически первым способом сведения задачи с ограничениями к задаче безусловной оптимизации явилось использование функции Лагранжа L(x,m)

L(x, m) = f(x) + m^т(b - j(x)) = f(x) + 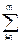m_i (b_i - j _i(x)),

где m_i ≥ 0, i=1,...,m - множители Лагранжа.

В соответствии с теоремой Куна-Таккера необходимым и достаточным условием оптимальности является то, что точка (x^*,m^*) седловая точка функции Лагранжа, т.е. удовлетворяет условию

max min L(x, m) = L(x*, m*) = min max L(x, m)

x m m x

При фиксированном m левая часть представляет собой прямую задачу математического программирования, при фиксированном x правая часть представляет собой двойственную задачу. На этой основе можно строить итеративный процесс, когда на каждом k-м шаге при фиксированных x^k и m^k решается пара двойственных задач вида

x^k+1 = arg max L(x, m^k) и m^k+1 = arg min L(x ^k, m)

x≥0 m≥0

Эти задачи являются задачами безусловной оптимизации и могут решаться, например, градиентными методами. Тогда

x^k+1 = (x^k + A_k Ñ_xL(x^k,m^k))⁺,

m^k+1 = (m^k - B_k Ñ_mL(x^k,m^k))⁺,

здесь A_k, B_k - шаговые множители; операция (⁺) позволяет обеспечить выполнение условий x≥0, m≥0 и имеет следующий смысл

x_i^k+1 = max {0,x_i^k + A_k Ñ_xL(x_i^k,m^k)},

m_i^k+1 = max {0, m_i^k - B_k Ñ_mL(x^k,m_i^k).

Метод характеризуется достаточно медленной сходимостью, однако, существуют способы увеличения скорости сходимости к оптимальному решению за счет специального выбора значений шаговых множителей A_k, B_k.