Постановка задачи целочисленного программирования

 

Первые упоминания о линейных уравнениях возникли ещё за несколько веков до нашей эры.

В Древней Греции Диофант (II-III в.) формулирует уравнения, в которых искомые переменные – целые. Например, для уравнения первой степени, а₀+а₁х₁=0, где а₀, а₁ – целые, решение х₁ = а₀/а₁ – целое, если а₀ делится на а₁ без остатка, т.е. такое уравнение не всегда разрешимо в целых числах. Из двух уравнений 3х₁–27=0 и 5х₂+21=0 только первое имеет целое решение: х₁=27/3=9, а второе – нет, так как х₂=–21/5.

Для уравнения с двумя неизвестными: а₁х₁+а₂х₂=0, где а₁, а₂ – целые, решение будет х₁=–(а₂/а₁)х₂. Например,

10х₁–5х₂ = 0 или х₁=0,5х₂. (1)

Из этого примера можно сделать следующие выводы: уравнение имеет бесчисленное множество решений, так как п > т; решение – целое, если х₂ – чётное.

Для того, чтобы из множества допустимых решений выбрать одно – оптимальное, необходимо, как нам уже известно, добавить к условию (1) целевую функцию. Задачи оптимизации, в которых решение должно быть в целых числах, называют задачами целочисленного программирования. Если в этой задаче целевая функция и ограничения – линейные зависимости, то её называют целочисленной задачей линейного программирования; если же хотя бы одна зависимость будет нелинейной, то такая задача формулируется как целочисленная задача нелинейного программирования.

Большинство практических задач принятия решения сводятся, как правило, к целочисленным задачам линейного программирования.

Если к условию (1) добавить такие, например, граничные условия:

2 £ х₁ £8; 1£ х₂ £ 3,

то можно видеть, что такая система решения не имеет. Отсюда следует, что задача целочисленного программирования не всегда имеет решения, т.е. она не совместна.

Под целочисленным или дискретным программированием понимают такие задачи (обычно линейные), в которых искомые переменные по смыслу могут принимать только целые значения: число рабочих, разделяемых по рабочим местам, количество единиц оборудования, устанавливаемых на заданной площади и т.п.

Аналитическая задача целочисленного программирования формулируется:

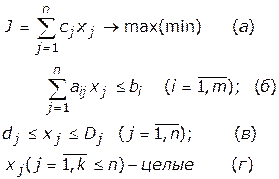(2)

Система (2) с точки зрения зависимостей ничем не отличается от задачи линейного программирования. Единственное отличие заключается в том, что в ней есть строка 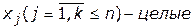, которая оказывает существенное влияние на решение задачи и значительно его усложняет. Число целочисленных переменных может удовлетворять одному из двух вариантов. Если 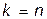, где — общее число всех переменных, то в ответе все переменные должны быть только целыми. В таком случае задачу называют полностью целочисленной. Если 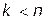, в ответе только 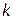переменных должны быть целыми, а остальные в заданных граничных условиях могут принимать любые значения. Иными словами, в ответе должны быть целые (но не все). В этом случае задачу называют частично целочисленной.

Следует отметить, что для решения задачи все целочисленные переменные обязательно должны иметь верхнюю границу.

Решение целочисленных и непрерывных задач оптимизации имеет принципиальные различия. Суть их заключается в следующем. Непрерывные задачи решают симплекс-методом с применением так называемых симплекс-таблиц. Каждой итерации соответствует своя симплекс-таблица. Есть признаки, с помощью которых по симплекс-таблицу можно получить ответы на вопросы: имеет ли вообще задача допустимое решение; является ли решение на данной итерации допустимым; является ли решение на данной итерации оптимальным.

Если задача имеет решения, то она решается до тех пор, пока не будут удовлетворены признаки этих решений. При этом решение является допустимым, если удовлетворяется один признак, и оптимальным, если удовлетворяются оба признака. К сожалению, для целочисленных задач таких признаков нет. Поэтому по задаче нельзя судить, во-первых, имеет ли она вообще допустимое решение и, во-вторых, является ли полученное допустимое решение оптимальным.

Некоторые вопросы, связанные с решением целочисленных задач, рассмотрим на таком примере:

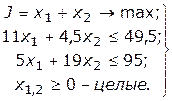
Решим эту задачу графически. Графическое решение целочисленной задачи включает следующие этапы: графическое решение непрерывной задачи; наложение требований целочисленности; анализ полученных результатов. Графическое решение непрерывной задачи показано на рис. 3.4.1.

Рис. 3.4.1.

 

Требование целочисленности переменных состоит в том, что решением задачи могут быть только точки, находящиеся на пересечении целочисленных значени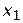й и .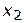

Из рис. 3.4.1 видно, что оптимальным решением задачи без учета требований целочисленности являются координаты точки 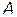, приведенные в табл. 3.4.1. Как следует из этой таблицы, значения 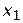и 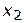в точке 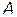требованиям целочисленности не удовлетворяют. Естественная попытка получить целочисленное решение сводится к округлению непрерывных значений. Округленные координаты, принадлежащие точке , оказываются за пределами ОДР, т. е. являются недопустимым решением. Предположение, что решение недопустимое, потому что округление было произведено в большую сторону, неверно. В точке координаты также округлены в большую сторону, а решение допустимое. И, наконец, из рис. 3.4.1 видно, что оптимальным решением будут координаты точки 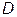, которые не являются ближайшими к непрерывному оптимальному решению.