Принцип В.Парето в задачах многокритериального выбора
В п. 4.1 было установлено, что для корректного решения задач многокритериального выбора необходимо в исходную постановку задачи (4.1)‑(4.2) привнести дополнительную информацию, позволяющую провести ее регуляризацию и построить результирующее отношение предпочтения. Данная информация может задаваться по-разному. Наиболее глубокий подход к построению 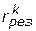 предполагает выяснение возможности подчинения этого построения определенной аксиоматике. Одна из известных систем аксиом была сформулирована Эрроу. Важное место среди других аксиом принадлежит аксиомам, связанным с принципом Парето. Данный принцип в общем случае может быть сформулирован с использованием двух определений.
предполагает выяснение возможности подчинения этого построения определенной аксиоматике. Одна из известных систем аксиом была сформулирована Эрроу. Важное место среди других аксиом принадлежит аксиомам, связанным с принципом Парето. Данный принцип в общем случае может быть сформулирован с использованием двух определений.
Определение 4.1. Альтернативы 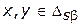 удовлетворяют отношению доминирования по Парето
удовлетворяют отношению доминирования по Парето  , тогда и только тогда, когда хотя бы по одному входному отношению предпочтения
, тогда и только тогда, когда хотя бы по одному входному отношению предпочтения  имело место доминирование (
имело место доминирование ( , где
, где  ‑ отношение строгого порядка), а по остальным ‑ безразличие или доминирование.
‑ отношение строгого порядка), а по остальным ‑ безразличие или доминирование.
Данное определение можно задать в виде единого соотношения вида:
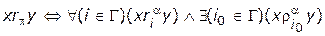 .
.
Определение 4.2. . Альтернативы 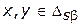 удовлетворяют отношению сильного доминирования по Парето
удовлетворяют отношению сильного доминирования по Парето 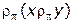 тогда и только тогда, когда по каждому входному отношению предпочтения
тогда и только тогда, когда по каждому входному отношению предпочтения 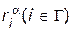 имеет место доминирование:
имеет место доминирование:  .
.
Данное определение также можно задать с использованием единого соотношения вида:
 .
.
Отношение доминирования по Парето в задачах многокритериального выбора при задании исходных отношений предпочтения 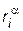 с использованием функций (функционалов)
с использованием функций (функционалов) 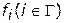 и с учетом принятых ранее требований их максимизации
и с учетом принятых ранее требований их максимизации  запишется следующим образом:
запишется следующим образом:
 .
.
Перечисленные представления принципа Парето, во-первых, определяют паретовскую аксиоматику, которой в числе прочих должно удовлетворять результирующее отношение предпочтения, и, во-вторых, используя (4.4)–(4.6) можно непосредственно осуществлять построение результирующего отношения предпочтения.
Замечание. Везде далее при постановке и решении задач многокритериального выбора будем предполагать выполненной (справедливой) аксиому независимости от непричастных альтернатив. Из данной аксиомы следует, что результат сравнения альтернатив 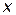 и
и 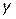 зависит только от них и не зависит от наличия или отсутствия некоторой третьей альтернативы
зависит только от них и не зависит от наличия или отсутствия некоторой третьей альтернативы 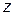 . Данная аксиома независимости должна восполняться и для соответствующих критериальных функций. Поясним это на примере.
. Данная аксиома независимости должна восполняться и для соответствующих критериальных функций. Поясним это на примере.
Пример 4.3. Пусть при управлении СТС ЛПР руководствуется тремя показателями (критериальными функциями): 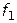 — характеризует общий объем выполненных операций,
— характеризует общий объем выполненных операций, 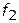 — характеризует время, оставшееся до конца планового периода управления,
— характеризует время, оставшееся до конца планового периода управления, 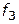 — оценивает дополнительные затраты, связанные с обеспечением выполнения запланированных операций.
— оценивает дополнительные затраты, связанные с обеспечением выполнения запланированных операций.
Если объем выполненных операций высок и имеется большой резерв времени до момента времени  , то дополнительно активизировать деятельности СТС нет необходимости, т.е. ЛПР будет предпочитать меньшие значения
, то дополнительно активизировать деятельности СТС нет необходимости, т.е. ЛПР будет предпочитать меньшие значения 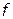 большим. Если выполнение комплекса операций под угрозой (недопустимо низкие значения
большим. Если выполнение комплекса операций под угрозой (недопустимо низкие значения 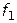 и
и 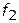 ), то ЛПР скорее всего предпочтет увеличение
), то ЛПР скорее всего предпочтет увеличение 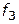 (увеличение дополнительных затрат), а не срыв выполнение боевой задачи. Таким образом, направление предпочтения по показателю
(увеличение дополнительных затрат), а не срыв выполнение боевой задачи. Таким образом, направление предпочтения по показателю 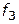 зависит от того, какие значения принимают показатели
зависит от того, какие значения принимают показатели 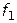 и
и 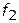 .
.
Показатель 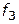 называется зависимым по предпочтению от остальных показателей. Используя приведенные выше правила определения предпочтительности альтернатив, принадлежащих множеств
называется зависимым по предпочтению от остальных показателей. Используя приведенные выше правила определения предпочтительности альтернатив, принадлежащих множеств  , можно в указанном множестве выделить множество недоминируемых (по Парето) или, по-другому, множество Парето, которое в дальнейшем будем обозначать следующим образом:
, можно в указанном множестве выделить множество недоминируемых (по Парето) или, по-другому, множество Парето, которое в дальнейшем будем обозначать следующим образом:  . Замечательное свойство множества Парето состоит в том, что если это множество не пусто, то всякая альтернатива, лежащая вне множества Парето, доминируется альтернативой, принадлежащей последнему множеству. Следовательно, рационально поиск наилучших, в том или ином смысле, альтернатив сосредоточить именно в области Парето. Так как точки множества Парето не доминируют друг с друга, то переход между этими точками может привести при решении задач векторной оптимизации к улучшению результатов по одним критериальным функциям
. Замечательное свойство множества Парето состоит в том, что если это множество не пусто, то всякая альтернатива, лежащая вне множества Парето, доминируется альтернативой, принадлежащей последнему множеству. Следовательно, рационально поиск наилучших, в том или ином смысле, альтернатив сосредоточить именно в области Парето. Так как точки множества Парето не доминируют друг с друга, то переход между этими точками может привести при решении задач векторной оптимизации к улучшению результатов по одним критериальным функциям  лишь при ухудшении результатов по другим
лишь при ухудшении результатов по другим  . Таким образом, окончательный выбор во множестве Парето связан с достижением определенного компромисса. Поэтому данное множество получило также название множества (области) компромиссов.
. Таким образом, окончательный выбор во множестве Парето связан с достижением определенного компромисса. Поэтому данное множество получило также название множества (области) компромиссов.
Дадим строгое определение понятию эффективной (недоминируемой по Парето) альтернативы.
Определение 4.3. Альтернатива 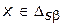 называется эффективной(недоминируемой), если во множестве допустимых альтернатив не существуют решения, которое доминирует по Парето альтернативу
называется эффективной(недоминируемой), если во множестве допустимых альтернатив не существуют решения, которое доминирует по Парето альтернативу  .
.
Определение эффективной альтернативы формально можно записать в следующем виде:
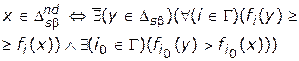
| (4.7) |
Следует отметить, что в отдельных монографиях или статьях эффективную (недоминируемую) альтернативу также называют паретовской, неулучшаемой альтернативой.
Приведем три примера, иллюстрирующих введенные выше понятия.
Пример 4.4. В задачах группового выбора часто используют графический способ задания отношений предпочтения 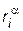 на множестве допустимых альтернатив. В этом случае альтернативам соответствуют вершины соответствующих графов, а ребра задают отношения предпочтения. На рисунке 4.2 а,б,в,г приведены варианты задания множества
на множестве допустимых альтернатив. В этом случае альтернативам соответствуют вершины соответствующих графов, а ребра задают отношения предпочтения. На рисунке 4.2 а,б,в,г приведены варианты задания множества 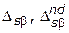 . Элементы множества
. Элементы множества 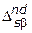 на рисунках помечены крестиками.
на рисунках помечены крестиками.
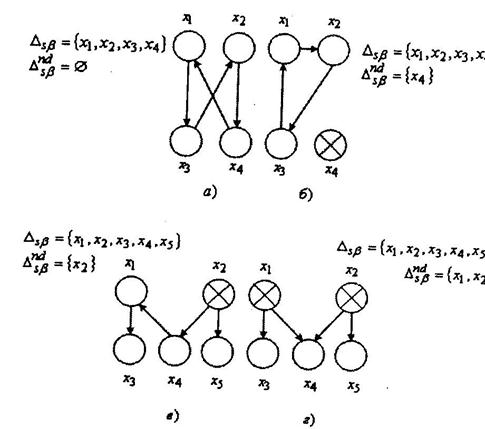
Рис. 4.2.
Пример 4.5. Пусть имеется три допустимых варианта создания СТС  , каждый из которых характеризуется вектором критериальных функций (вектором показателей эффективности):
, каждый из которых характеризуется вектором критериальных функций (вектором показателей эффективности): 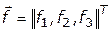 , причем
, причем 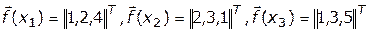 . Так как каждая компонента вектора
. Так как каждая компонента вектора 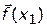 доминируется соответствующими компонентами вектора
доминируется соответствующими компонентами вектора  , то альтернатива
, то альтернатива  ; альтернативы
; альтернативы 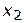 и
и  не доминируют друг друга, т.к.
не доминируют друг друга, т.к.  , но
, но 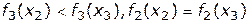 . Поэтому
. Поэтому  .
.
Пример 4.6. В двухкритериальных задачах линейного программирования с двумя неизвестными можно достаточно наглядно представить множество Парето (множество компромиссов) как в пространстве альтернатив, так и в пространстве целевых функций. В самом деле, пусть 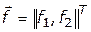 , где
, где
 .
.
Множество допустимых альтернатив в рассматриваемой задаче зададим в виде системы линейных неравенств:  . Тогда по аналогии с рисунком 4.1 зададим в пространстве альтернатив и критериальных функций соответствующие множества, которые в графическом виде представим на рисунке 4.3.
. Тогда по аналогии с рисунком 4.1 зададим в пространстве альтернатив и критериальных функций соответствующие множества, которые в графическом виде представим на рисунке 4.3.

Рис. 4.3.
На рисунке 4.3 области Парето альтернатив в пространстве и образ области Парето критериальных функций изображены на качественном уровне (без указания конкретных координат характерных точек указанных множеств). При этом в пространстве  множеству Парето принадлежат точки, лежащие на гранях
множеству Парето принадлежат точки, лежащие на гранях 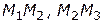 . Точка
. Точка  является неэффективной, так как доминируется, например, точкой
является неэффективной, так как доминируется, например, точкой  . В пространстве критериальных функций
. В пространстве критериальных функций 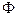 образами точек, принадлежащих граням
образами точек, принадлежащих граням 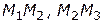 , являются точки, принадлежащие граням
, являются точки, принадлежащие граням  , которые, в свою очередь, образуют образ множества Парето в пространстве целевых функций. Конкретный вариант задания указанных множеств для задач линейного программирования будет приведен в конце данной главы.
, которые, в свою очередь, образуют образ множества Парето в пространстве целевых функций. Конкретный вариант задания указанных множеств для задач линейного программирования будет приведен в конце данной главы.
Важным практическим результатом выделения области компромиссов (множества Парето) является существенное сужение области поиска оптимальных решений. В связи с этим весьма актуально и полезно получать в явном виде решения из области компромиссов и предъявлять их ЛПР. Для этого необходимо изучить свойства множества Парето и методы его построения.