Основные свойства множества Парето

Рассмотрим основные свойства множества Парето (множества 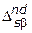и соответственно 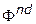). При этом, как и ранее будем предполагать, что все целевые функции максимизируются.

Свойство № 1. Никакие альтернативы, принадлежащие множеству допустимых альтернатив , не доминируют (не превосходят) альтернативы, принадлежащие множеству Парето.

Свойство № 2. При переходе от одной точки (альтернативы) множества Парето к другой точке множества Парето происходит увеличение значений одних критериальных функций и уменьшение значений других критериальных функций.

Свойство № 3. Множеству Парето принадлежат все альтернативы 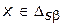, при которых достигается единственные (или глобальные) экстремумы значений хотя бы одной из критериальных функций 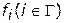, как при отсутствии ограничений на значения остальных критериальных функций, так и при вводе (частичном вводе) таких ограничений. Другими словами, множеству Парето принадлежат альтернативы 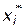, для которых

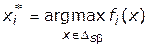
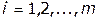Свойство № 4. Множеству Парето принадлежат все точки 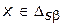, в которых достигается единственный (или глобальный) экстремум линейных форм вида

(4.8)

где 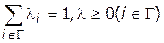. При этом должно быть ограниченным и замкнутым множеством (компакт), а функции 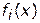непрерывны.

Свойство № 5. Если множество альтернатив 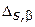является выпуклым компактом и соответствующим требованиям вогнутости (выпуклости) удовлетворяют непрерывные функции 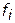, то решение совокупности указанных выше экстремальных задач вида (4.8) в принципе определяет все точки множества Парето.

Важное свойство множества, не связанное с предположением о выпуклости 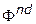, было обнаружено Ю.Б. Гермейером.

Свойство № 6. Любая точка множества Парето, расположенного в строго положительном варианте, может быть представлена как решение задачи

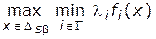(4.9)

при соответствующем подборе коэффициентов, на которые накладывается условие 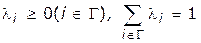. При этом — компакт, 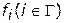непрерывны.

Важную роль в задачах векторной оптимизации играет точка в пространстве критериальных функций 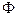, в которой все критериальные функции принимают экстремальные значения (в данном случае максимальные значения). Пусть 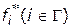— максимальные значения каждой критериальной функции. Эта точка может иметь прообраз в пространстве альтернатив 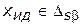в том идеальном случае, при котором в этой точке одновременно достигается максимум по всем указанным функциям. На рисунке 4.3 данная точка обозначена вектором 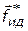. На рисунке 4.4 изображена ситуация, при которой точка 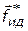имеет прообраз (точку) в пространстве альтернатив, которая является единственной точкой множества Парето. Данную точку 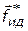называют идеальной (утопической) точкой множества Парето. Нахождение идеальной точки во многих случаях оказывается весьма полезным при постановке задач определения реальной точки выбора. Кроме того, компоненты утопической точки 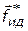часто используют для нормализации соответствующих критериальных функций.

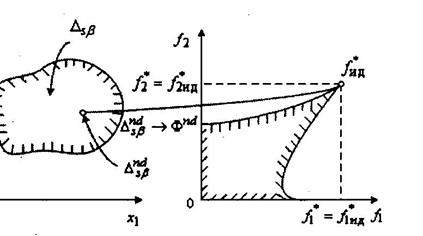
Рис. 4.4.

В заключение данного подпункта остановимся на особенностях графического задания множеств 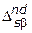и 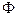. Так, например, в случае решения двух или трех критериальных задач можно непосредственно находить точки множества Парето на основе анализа соответствующих графиков, задающих множество эффективных оценок. Данный подход лежит в основе реализации методов решения задач, в которых осуществляется оптимизация показателей, оценивающих эффективность и стоимость создания и применения, сложных организационно-технических систем. На рисунке 4.5 для примера построен график шести вариантов СТС, каждый из которых характеризуется своей стоимостью создания и эксплуатации (показатель 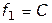) и эффективностью применения (показатель ).

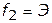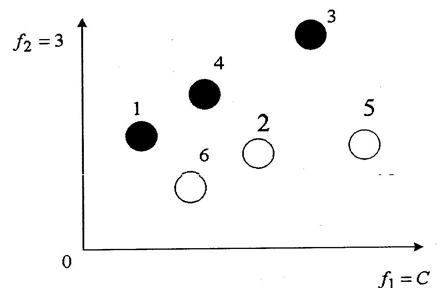
Рис. 4.5.

Так показатель 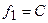желательно минимизировать, а показатель 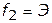максимизировать, то из рисунка 4.5 следует, что четвертый вариант СТС предпочтительнее второго варианта (последний имеет меньшую эффективность и в то же время большую стоимость). Таким образом, из шести представленных вариантов СТС лишь три (первый, четвертый и третий) могут претендовать на роль лучшего и являются недоминируемыми альтернативами. Обобщением рассматриваемого подхода к изображению множества Парето является подход, в котором наряду с двумя перечисленными критериальными функциям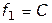и и 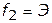вводится еще одна критериальная функция 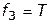, где 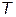— время жизненного цикла соответствующей СТС. В этом случае график векторных оценок оказывается пространственным и изображается в наиболее наглядной плоской проекции или же представляется несколькими плоскими сечениями.

В том случае, если число критериальных функций больше трех, для графического представления пространства критериальных функций широко используют полярные и линейные диаграммы. На рисунках 4.6, 4.7 для примера проведено сравнение двух проектов создания программно-математического обеспечения АСУ (варианты 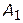и ) с использованием полярных диаграмм (диаграмм Кивиата) и линейных диаграмм. При этом рассматриваются восемь основных критериальных функции [1,16]: 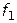— основная стоимость; 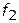— полная стоимость; 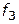— сроки создания; 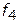— точность удовлетворения требований; 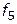— приватность; 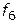— сопровождаемость; 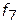— детализация; 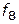— показатель, характеризующий рост штата сотрудников. На радиальных лучах диаграммы откладываются как числовые значения соответствующих показателей (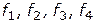), так качественные характеристики (градации, уровни): неприемлемый, приемлемый, промежуточный, желательный. В этом случае лучшей альтернативой является та, которой соответствует большая область круга, или та, которая по форме лучше приближается к окружности. Представление альтернатив с использование линейных диаграмм (рисунок 4.7) менее наглядно по сравнению с полярными диаграммами. Однако в этом случае построение соответствующих графиков проводить проще, а добавление новых критериальных функций не требует перестройки всего графика, как это приходится делать в случае полярных диаграмм.

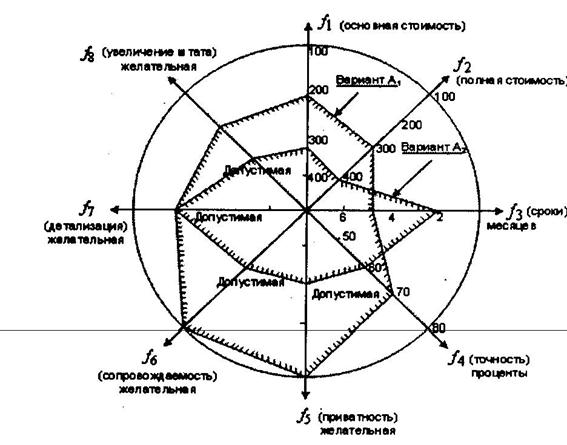
Рис. 4.6.

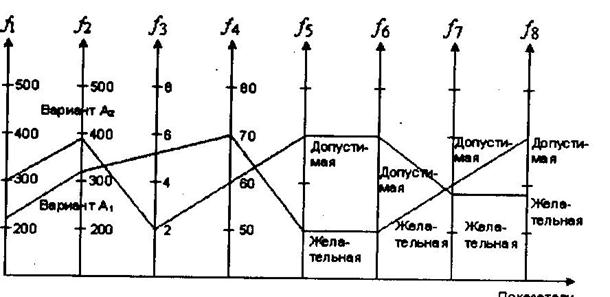
Рис. 4.7.