Методы построения множества Парето

 

Приведенные в п.4.2.2 свойства множества Парето могут быть использованы для построения (исследования) данного множества (либо его подмножеств) или определения его характеристик в конкретных прикладных задачах. При этом большинство методов определения указанного множества 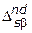основано на сформулированных условиях оптимальности. Чаще всего используются необходимые условия оптимальности, состоящие в том, что если точка эффективна (в том или ином смысле), то она является решением задачи максимизации или минимизации (возможно, при некоторых дополнительных ограничениях) числовой функции специального вида при надлежащим образом назначенных величинах параметров, входящих в эту функцию и (или) ограничения.

В этом случае задача выделения всех эффективных решений сводится к соответствующей скалярной параметрической задаче математического программирования. Указанную замену исходной задачи векторной оптимизации параметрическим семейством обычных экстремальных задач часто называют скаляризацией исходной задачи. Однако в этом случае получаемое множество может содержать «лишние» точки, которые не являются эффективными и поэтому должны быть выявлены и отсеяны. Если при поиске множества 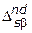используют достаточные условия оптимальности, то решения соответствующих скалярных параметрических задач, удовлетворяющие им, являются эффективными.

К настоящему времени наиболее конструктивные результаты, связанные с построением множества Парето, получены для случаев, когда 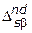компактно и выпукло, а непрерывные функции 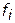вогнуты. В этом случае оказываются справедливы свойства 4 и 5, которым должны удовлетворять все точки множества Парето. Алгоритм поиска указанных точек сводится к решению следующей совокупности экстремальных задач:

(4.12)

Последовательно перебирая значения 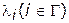, можно получать точки множества Парето. Геометрическая интерпретация данного процесса сводится к построению опорных гиперплоскостей к множеству допустимых значений критериальных функций 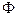. На рисунке 4.8 показан для случая двух критериальных функций пример построения двух линий уровня, которые касаются множества 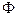в точках, принадлежащих 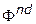. Следует подчеркнуть, что требование выпуклости и вогнутости 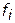существенно, т.к. если данные требования не выполняются, то решение задач (4.12) не гарантирует получение всех точек множества Парето. Это иллюстрируется геометрическим примером, представленным на рисунке 4.9. На данном рисунке точки множества 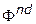, выделенные штриховой линией, не могут быть выделены ни при каких коэффициентах 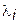в задаче (4.12).

Рис. 4.8.

 

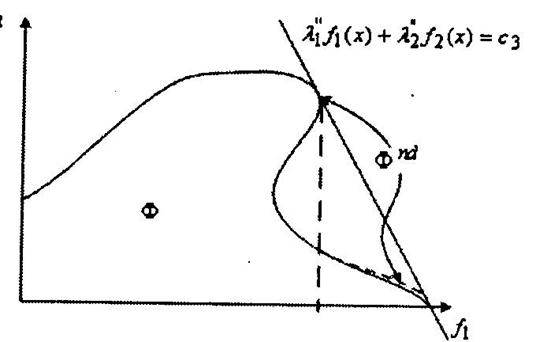
Рис. 4.9.

 

Частным случаем постановки задачи (4.12) является задача многокритериального линейного программирования, в которой множество ограничено выпуклой оболочкой, натянутой на конечное множество точек (вершин), называемой выпуклым многогранником [15, 24]. При этом все 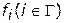линейны. Вершины рассматриваемого выпуклого многогранника, образующие конечное множество 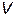, и являются объектом первоначального исследования.

Цель этого исследования состоит в выявлении всех вершин, принадлежащих к множеству недоминируемых решений 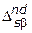. Эти вершины образуют конечное множество 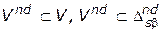. В частности, очевидно, что к множеству 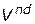принадлежат все вершины, в которых достигаются экстремумы по каждой целевой функции 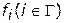в отдельности.

При поиске элементов 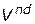используется ряд свойств этого множества. Среди них наиболее важным для практических приложений является свойство связности, т.е. возможности последовательного перехода между точками через такие соседние вершины, которые также принадлежат к 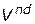. На основе данного свойства была разработана комбинаторная симплекс-процедура для отыскания всех точек множества 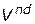. Эта процедура связана с запоминанием всех базисов выявленных точек 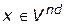и с определением на каждом шаге соответствующим образом модифицированным симплекс-методом новой точки 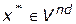при проведении перебора указанных базисов.