Методы построения результирующих отношений предпочтения на основе свертки показателей
Сущность данных методов многокритериальной оптимизации состоит в построении такого результирующего отношения предпочтения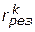 
(в частности, результирующей целевой функции 
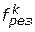), на основе которого возможно прямое выделение во множестве 
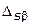оптимальной в некотором смысле альтернативы 
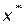. В связи с этим данные методы называют еще и прямыми методами векторной оптимизации. В общем случае при реализации указанных методов выделяется некоторое подмножество альтернатив 
, относительно которых нельзя однозначно сказать о том, что они являются паретооптимальными. Поэтому на втором этапе реализации данных методов необходимо проводить проверку выделенных альтернатив 
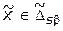на паретооптимальность с использованием условий, перечисленных ранее в п.4.2.2, 4.2.3. Указанная особенность приводит к тому, что многие из прямых методов векторной оптимизации по существу совпадают с некоторыми из методов определения точек во множестве Парето (см. п.4.2.3).
При применении прямых методов часто осуществляется модификация функций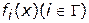 
как в интересах приведения всех функций к однородному (нормализованному) виду, так и в целях видоизменения содержательного характера этих функций. Данная модификация необходима, т.к. в большинстве случаев масштабы измерения критериальных функций 
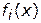неодинаковы и требуется искусственно приводить их к одной мере. Обозначим через 
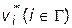— максимально возможные значения функций 
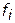, а через 
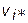— минимально допустимые (минимально целесообразные) значения этих функций. В частности в качестве 
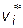и 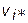могут соответственно приниматься максимальные 
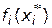и минимальные 
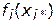значения, достигаемые функцией 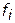во множестве Парето, либо соответственно 
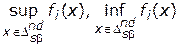[17].
С учетом введенных обозначений основные виды модификаций могут быть представлены следующим образом:
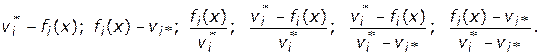
В дальнейшем будем обозначать модифицированные функции через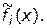 
В качестве первых примеров свертки, используемых в прямых методах векторной оптимизации, рассмотрим следующие варианты задания результирующих функций выбора
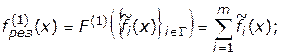(4.36)
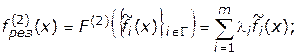(4.37)
где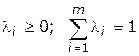 
. Соответствующий такому представлению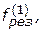 
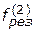принцип оптимальности или, по-другому, правило согласования 
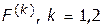альтернатив 
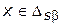носит название принципа равномерной оптимальности.
Содержательное обоснование правомерности использования данного принципа оптимальности оказывается убедительным для задач, где оценки альтернатив по каждой критериальной функции могут быть выражены (численно и в смысловом плане) в единицах оценок по какой-либо одной критериальной функции-компоненте векторного показателя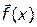 
[17]. Наиболее характерными примерами таких задач являются задачи с показателями, допускающими стоимостное выражение. В этом случае сумма значений частных критериальных функций вида (4.36), (4.37), выраженная в денежных единицах, может рассматриваться как доход (либо потери) от выбора альтернативы 
.
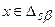Основными недостатками данного варианта свертки являются [10,17]:
1) слабая связь весовых коэффициентов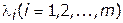 
с действительной ролью частных критериальных функций 
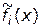при обобщенной оценке альтернатив с использованием 
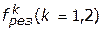. При этом введение весовых коэффициентов лишь создает видимость большей объективности формулы (4.37), однако их определение сталкивается с серьезными трудностями;
2) трудность отыскания объективного способа нормирования частных критериальных функций 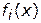для приведения их к безразмерному виду, т.к. значимость каждой 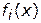определяется величинам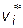и и ;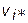
3) возможность компенсации недопустимо малых значений оценок альтернатив по некоторым критериальным функциям большими значениями по другим критериальным функциям.
Из-за последнего недостатка при решении конкретных задач векторной оптимизации с использованием соотношений (4.36) могут получаться абсурдные результаты. Проиллюстрируем это на простейшем примере.
Пример 4.8. Пусть переменная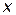 
— характеризует конкретный вариант проекта самолета, 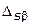— конечное множество указанных вариантов, критериальные функции 
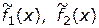позволяют оценить соответственно надежность и скорость движения проектируемого самолета. Тогда можно выбрать такой вариант самолета 
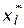, который будет обладать наивысшей надежностью 
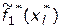(из-за многократного резервирования всех основных деталей и узлов), но обладать нулевой скоростью 
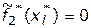. При этом
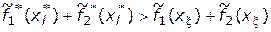, (4.38)
.
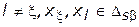Другим вариантом задания результирующей функции выбора в задачах векторной оптимизации является вариант, при котором
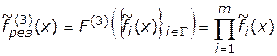. (4.39)
Выражение (4.39) представляет собой свертку‑произведение оценок альтернатив по всем критериальным функциям. Принцип оптимальности, реализуемый с использованием данного варианта свертки, называется принципом справедливого компромисса и формулируется следующим образом: справедливым следует считать такой компромисс, когда суммарный уровень относительного снижения одной или нескольких критериальных функций не превышает суммарного уровня относительного увеличения остальных критериальных функций.
При этом существуют содержательные схемы рассуждений, обусловливающие правомочность использования принципа справедливого компромисса в конкретных задачах [13,14]. Так, если использовать данный принцип решения задачи выбора варианта самолета (см. пример 4.8), то при этом альтернатива 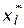никогда не будет рекомендована, т.к. 
.
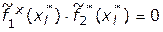Вместе с тем, рассматриваемый принцип также имеет ряд недостатков [13,14]:
1) возможна компенсация недостаточных значений величины одной критериальной функции 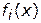— избыточными значениями величин другой (других) критериальных функций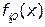 
;
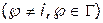2) происходит выравнивание (сглаживание) значений частных критериальных функций.
В выражении (4.39) можно учесть важность отдельных критериальных функций следующим образом:
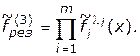(4.40)
Более сложный вариант свертки в задачах векторной оптимизации определяется с использованием следующей результирующей функции выбора [13,14]
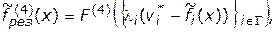(4.41)
где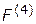 
— интерпретируется как расстояние между идеальной (номинальной, целевой) точкой 
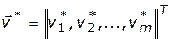и точкой 
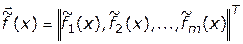, задаваемое с использованием конкретной метрики. Данный класс задач векторной оптимизации
получил название задач целевого программирования [13,14]. Примером конкретного варианта задания 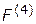может служить вариант, при котором:
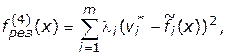(4.42)
где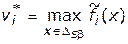 
— 
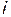-ая компонента идеальной (утопической) точки. Достоинство использования моделей и методов целевого программирования состоит в том, что они имеют наглядную содержательную интерпретацию для ЛПР и опираются на достаточно богатый методический и программный задел решения однокритериальных задач вида (4.41), (4.42).
Однако при использовании указанного варианта свертки требуется дополнительная информация для обоснования самой идеальной (целевой) точки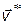 
и соответствующей метрики в пространстве критериальных функций. Опыт показывает, что использование разных метрик приводит в общем случае к разным решениям задач векторной оптимизации. Кроме того, выбор в качестве 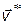утопической точки 
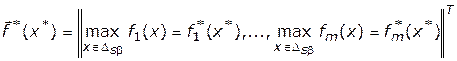может приводить, вообще говоря, к нарушению аксиомы независимости, о которой речь шла в п. 4.2.1.
Анализ перечисленных выше вариантов решения задач многокритериальной оптимизации показывает, что при использовании (априорных) методов многокритериального принятия решений выбор соответствующего принципа оптимальности существенно зависит от типа и структуры конкретно решаемой задачи [13,14]. Имеющийся положительный опыт использования какого-либо принципа оптимальности в конкретных задачах (одной или нескольких) не являются основанием его применения в других задачах. Если это обстоятельство не учитывать, то возможна некорректная регуляризация исходной задачи, т.е. принимаемый принцип оптимальности и выбираемая согласно ему альтернатива 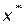не будут соответствовать целевой установке решаемой задачи. Однако, к сожалению, в априорных методах многокритериальной оптимизации не предусмотрено этапа и средств дополнительного анализа исходной задачи многокритериального выбора, обеспечивающих ее корректную регуляризацию. Указанные средства присутствуют в апостериорных и адаптивных методах векторной оптимизации, но для их реализации требуется дополнительная информация, получаемая от ЛПР, экспертов, что значительно усложняет процедуру поиска эффективных альтернатив.