Анализ существования решений в задаче линейного программирования

Рассмотрим неравенство ах £ b. Если от неравенства мы хотим перейти к уравнению, то введём дополнительную переменную у и запишем ах +у = b, т.е. получим одно уравнение с двумя неизвестными.

В общую постановку задачи оптимизации входят неравенства вида 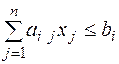(i =1...т), где п – число неизвестных; т – число неравенств. Если в каждое неравенство добавить неотрицательное неизвестное y_i ³ 0
(i = 1...m), то от системы неравенств можно перейти к системе уравнений (i = 1...m).

В этой системе общее число неизвестных N = n+m, где п – число основных неизвестных x_j; т – число дополнительных неизвестных y_i, которое равно числу уравнений.

Возможны три варианта соотношения величин N и т.

1. Число неизвестных меньше, чем число уравнений: N < m.

Например, 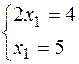, т.е. N =1, т =2. Очевидно, эта система решения не имеет, т.е. нет таких значений х₁, которые удовлетворяли бы обоим уравнениям. В этом случае говорят, что система условий несовместна. Значит, если число неизвестных N меньше числа уравнений т, то система решения не имеет и является несовместной.

2. Число неизвестных равно числу уравнений: N = m.

Например, . Нетрудно найти, что решением этой системы будут значения х₁ =2, х₂=1. Таким образом, линейная система, в которой число неизвестных N равно числу уравнений т, имеет одно решение.

Наличие (2) или отсутствие решений (1) при различных соотношениях числа переменных N и числа уравнений т справедливо только для линейно–независимых уравнений, которые не могут быть получены умножением, делением, сложением, вычитанием исходных уравнений.

Например, пусть есть уравнение 2х = 10, из которого можно получить несколько: х=5; 4х=20; 6х=30 и т.д. Все эти уравнения будут линейно зависимыми, и новых сведений о зависимостях для переменной не содержат. Поэтому в этом примере т=1 (а не 4).

Аналогично в системе

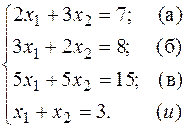
есть только два линейно независимых уравнения, так уравнение (в) есть результат суммирования (а) и (б), а уравнение (г) есть результат деления (в) на 5.

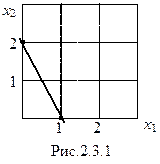3. Число неизвестных больше числа уравнений: N > m. Например,
2х₁ + х₂ = 2. Очевидно, что все значения х₁ и х₂, лежащие на прямой (рис.1.3.1) этого уравнения, являются его решением. Значит это уравнение имеет бесчисленное множество решений. Итак, если в системе число неизвестных N больше числа уравнений т, то такая система имеет бесчисленное множество решений.

В случае, когда система имеет более одного возможного решения, может быть поставлена задача оптимизации. При этом суть такой задачи, как мы уже знаем, заключается в том, чтобы из всех допустимых решений, удовлетворяющих ограничениям и граничным условиям, выбрать такое, которое придаёт ЦФ оптимальное, т.е. максимальное или минимальное значение.

Если все ограничения и ЦФ линейны, задача оптимизации, как нам известно, является задачей ЛП.