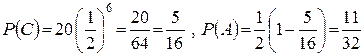Формула умножения вероятностей.
Пусть даны два события  и
и  . Рассмотрим событие
. Рассмотрим событие 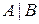 , состоящее в том, что событие
, состоящее в том, что событие  появилось после появления события
появилось после появления события  . Если
. Если 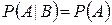 , то событие
, то событие  называется независимым от события
называется независимым от события  . В противном случае
. В противном случае 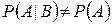 событие
событие  называется зависимым от события
называется зависимым от события  . Величина
. Величина 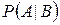 называется условной вероятностью события
называется условной вероятностью события  при появлении события
при появлении события  .
.
Теорема. Вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого события.
Доказательство: Рассмотрим схему случаев
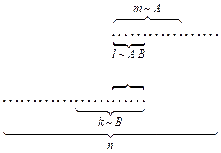
Вычисляя вероятности по этой схеме, получаем
 ,
,
таким образом
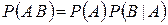 (1.8.1)
(1.8.1)
Что и требовалось доказать.
Совершенно аналогично доказывается вторая формула
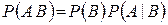 (1.8.2)
(1.8.2)
Следствие: Если событие  не зависит от события
не зависит от события  , то и событие
, то и событие  не зависит от события
не зависит от события  .
.
Доказательство: Дано 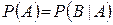 – независимость события
– независимость события  от события
от события  , по формуле умножения вероятностей имеем –
, по формуле умножения вероятностей имеем – 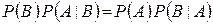 , отсюда следует, что
, отсюда следует, что  , то есть событие
, то есть событие  не зависит от события
не зависит от события  . Что и требовалось доказать.
. Что и требовалось доказать.
Для двух независимых событий имеет место формула
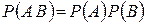 (1.8.3)
(1.8.3)
Для нескольких независимых событий имеет место аналогичная формула
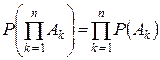 (1.8.4)
(1.8.4)
Рассмотрим примеры на применение теоремы сложения и умножения вероятностей.
Пример 1.8.1. В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Найти вероятность того, что оба шара белые.
Решение. Обозначим:  – появление двух белых шаров. Событие
– появление двух белых шаров. Событие  представляет собой произведение двух событий:
представляет собой произведение двух событий: 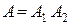 , где
, где 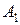 – появление белого шара при первом вынимании,
– появление белого шара при первом вынимании, 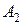 – появление белого шара при втором вынимании. По теореме умножения вероятностей
– появление белого шара при втором вынимании. По теореме умножения вероятностей 
Пример 1.8.2. Те же условия, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются.
Решение: В данном случае события независимы и 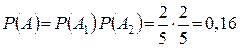
Пример 1.8.3. Прибор, работающий в течение времени 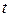 , состоит из трех узлов, каждый из которых, независимо от других, может в течение времени
, состоит из трех узлов, каждый из которых, независимо от других, может в течение времени 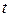 отказать (выйти из строя). Отказ хотя бы одного узла приводит к отказу прибора в целом. За время
отказать (выйти из строя). Отказ хотя бы одного узла приводит к отказу прибора в целом. За время 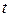 надежность (вероятность безотказной работы) первого узла равна 0,8; второго 0,9; третьего 0,7. Найти надежность прибора в целом.
надежность (вероятность безотказной работы) первого узла равна 0,8; второго 0,9; третьего 0,7. Найти надежность прибора в целом.
Решение. Обозначим:
 – безотказная работа прибора,
– безотказная работа прибора, 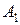 – безотказная работа первого узла,
– безотказная работа первого узла, 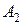 – безотказная работа второго узла,
– безотказная работа второго узла, 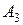 – безотказная работа третьего узла.
– безотказная работа третьего узла. 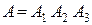
По теореме умножения для независимых событий имеем: 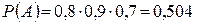
Пример 1.8.4. Производится три выстрела по одной и той же мишени. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно 0,4 ; 0,5 ; 0,7 . Найти вероятность того, что в результате этих трех выстрелов в мишени будет ровно одна пробоина ( хотя бы одна пробоина).
Решение. 1) Рассмотрим событие
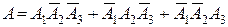
где 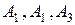 – попадание при первом, втором, третьем выстрелах,
– попадание при первом, втором, третьем выстрелах, 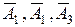 – промах при первом, втором, третьем выстрелах. Применяя теоремы сложения и умножения вероятностей и пользуясь свойством противоположных событий, находим
– промах при первом, втором, третьем выстрелах. Применяя теоремы сложения и умножения вероятностей и пользуясь свойством противоположных событий, находим 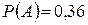 .
.
2) Рассмотрим событие  – хотя бы одно попадание в мишень.
– хотя бы одно попадание в мишень. 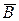 – ни одного попадания в мишень. Очевидно,
– ни одного попадания в мишень. Очевидно,  . По теореме умножения
. По теореме умножения  , откуда
, откуда 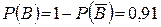 .
.
Пример 1.8.5. Монета бросается 6 раз. Найти вероятность того, что выпадет больше гербов, чем цифр.
Решение. Для нахождения вероятности интересующего нас события  (выпадет больше гербов, чем цифр) можно было бы перечислить все возможные его варианты, например, выпадет шесть гербов и ни одной цифры, выпадет пять гербов и одна цифра и т. д.
(выпадет больше гербов, чем цифр) можно было бы перечислить все возможные его варианты, например, выпадет шесть гербов и ни одной цифры, выпадет пять гербов и одна цифра и т. д.
Однако проще будет применить другой прием. Перечислим все возможные исходы опыта:  – выпадет больше гербов, чем цифр,
– выпадет больше гербов, чем цифр,  – выпадет больше цифр, чем гербов,
– выпадет больше цифр, чем гербов, 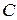 – выпадет одинаковое число цифр и гербов. События
– выпадет одинаковое число цифр и гербов. События 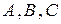 несовместны и образуют полную группу. Следовательно,
несовместны и образуют полную группу. Следовательно,  . Так как задача симметрична относительно «герба» и «цифры», то
. Так как задача симметрична относительно «герба» и «цифры», то 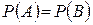 , откуда
, откуда
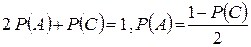
Найдем вероятность события С, состоящего в том, что при шести бросаниях монеты появится ровно три герба (а значит, ровно три цифры). Вероятность любого из вариантов события 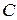 (например, последовательность – г, ц, г, г, ц, ц) при шести бросаниях одна и та же и равна
(например, последовательность – г, ц, г, г, ц, ц) при шести бросаниях одна и та же и равна 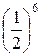 . Число таких комбинаций равно числу сочетаний трех из шести
. Число таких комбинаций равно числу сочетаний трех из шести 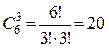 . Следовательно,
. Следовательно,