КОНСПЕКТ ЛЕКЦИЙ ПО МАТЕМАТИКЕ ТЕОРИЯ ВЕРОЯТНОСТЕЙ МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ И ИНФОРМАТИКИ

КОНСПЕКТ ЛЕКЦИЙ

ПО МАТЕМАТИКЕ

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

САМАРА 2006

СОДЕРЖАНИЕ

1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ. 3

1.1. Статистическое определение вероятности. 3

1.2. Пространство элементарных событий. 3

1.3. Действия на событиями. 4

1.4. Элементы комбинаторики. 5

1.4.1. Перестановки. 5

1.4.2. Размещения. 5

1.4.3. Сочетания. 6

1.5. Классическое определение вероятности. 6

1.6. Формула сложения вероятностей для несовместных событий. 7

1.7. Формула сложения вероятностей для произвольных событий. 7

1.8. Формула умножения вероятностей. 8

1.9. Формула полной вероятности. 10

1.10. Формула вероятностей гипотез (Байеса). 11

1.11. Повторение опытов. 12

1.11.1. Схема Бернулли. 12

1.11.2. Асимптотическая формула Муавра – Лапласа. 14

1.11.3. Асимптотическая формула Пуассона. 15

1.12. Случайные дискретные величины. 15

1.13. Случайные непрерывные величины. 16

1.14. Функция плотности вероятности случайной непрерывной величины. 17

1.15. Числовые характеристики случайных величин. 18

1.15.1.Мода случайных величин. 18

1.15.2. Квантили случайных величин. 19

1.15.3. Математическое ожидание случайных величин. 19

1.15.4. Среднеквадратичное отклонение и дисперсия случайных величин. 20

1.15.4. Моменты случайных величин. 21

1.16. Теоремы о числовых характеристиках случайных величин. 23

1.17. Законы распределения случайных величин. 24

1.17.1. Биномиальный закон распределения. 24

1.17.2. Закон распределения Пуассона. 25

1.17.3. Равномерный закон распределения. 26

1.17.4. Нормальный закон распределения. 27

1.17.5. Экспоненциальный закон распределения. 30

1.17.6. Гамма – распределение. 31

1.18. Системы случайных величин. 33

1.18.1. Система двух случайных дискретных величин. 34

1.18.2. Система двух случайных непрерывных величин. 35

1.18.3. Условные законы распределения. 37

1.18.4. Числовые характеристики системы двух случайных величин. 39

1.18.5. Система нескольких случайных величин. 41

1.18.6. Нормальный закон распределения системы двух случайных величин. 43

1.19. Предельные теоремы теории вероятностей. 45

1.19.1. Неравенство Чебышева. 45

1.19.2. Закон больших чисел. 46

1.19.3. Центральная предельная теорема. 47

2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. 47

2.1. Основные задачи математической статистики. 47

2.2. Простая статистическая совокупность. Статистическая функция распределения. 48

2.3. Статистический ряд. Гистограмма. 49

2.4. Числовые характеристики статистического распределения. 51

2.5. Выбор теоретического распределения по методу моментов. 52

2.6. Проверка правдоподобия гипотезы о виде закона распределения. 55

2.7. Критерии согласия. 56

2.8. Точечные оценки для неизвестных параметров распределения. 59

2.9. Оценки для математического ожидания и дисперсии. 59

2.10. Доверительный интервал. Доверительная вероятность. 62

 

ТЕОРИЯ ВЕРОЯТНОСТЕЙ.

Случайным называется явление, которое при проведении опыта может протекать каждый раз несколько по иному. Практика показывает, что наблюдение массы однородных случайных явлений… Примеры случайных явлений: Опыт Явление 1. Подбрасывание монеты Появление герба …

Статистическое определение вероятности.

Пусть в результате опыта может появится или не появится некоторое событие , обозначим – общее число опытов, – число появлений события . Отношение … (1.1.1) называется относительной частотой (или просто частотой) события . При неограниченном увеличении числа опытов частота…

Пространство элементарных событий.

1) в результате опыта появляется одно и только одно событие , 2) для любого события , связанного с данным опытом по наступившему событию… Тогда множество называется пространством элементарных событий. (Пример с окрашенным кубиком). Элементарные события…

Действия на событиями.

Произведением двух событий и называется новое событие , состоящее в…

Элементы комбинаторики.

Перестановки.

. (1.4.1) Пример 1.4.1. Сколько существует способов для расстановки десяти книг на… Пример 1.4.2. Сколько различных восьмизначных чисел можно составить из цифр 1,2,3,4,5,6,7,8?

Размещения.

(1.4.2) Пример 1.4.4. На юридическом факультете в группе 16 студентов, которые сидят… Пример 1.4.5. Сколько существует способов расстановки на полке 5 выбранных уголовных дел из 10 имеющихся?

Сочетания.

. (1.4.3) Пример 1.4.9. Восемнадцать студентов задержанных по подозрению в организации… Пример 1.4.10. Сколько различных опергрупп из 5 человек можно составить в отряде из 25 человек?

Классическое определение вероятности.

Пусть 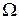– пространство из 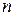элементарных событий. Если при этом все элементарные события являются равновозможными (равновероятными), то их называют случаями. Такой опыт называется схемой случаев. Пусть некоторому событию благоприятствует случаев. Классической вероятностью события называется отношение числа благоприятствующих случаев событию к общему числу опытов.

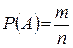(1.5.1)

Классическое определение вероятности не требует опытных данных (в этом его преимущество), но оно пригодно только для схемы случаев (в этом его недостаток). Логически статистическое и классическое определение вероятности независимы, но хорошо согласуются.

Пример 1.5.1. В урне находится 2 белых и 3 черных шара. Наугад вынимается один шар. Какова вероятность того, что этот шар будет белым?

Пример 1.5.2. Выбрасываются две игральные кости. Какова вероятность того, что выпадет сумма 7?

.

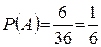Пример 1.5.3. В партии из изделий 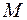бракованных. Из партии наугад выбирается 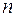изделий. Какова вероятность, что среди этих 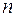будет ровно 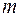бракованных?

Формула сложения вероятностей для несовместных событий.

(1.6.1) Доказательство: Рассмотрим схему случаев.

Формула сложения вероятностей для произвольных событий.

(1.7.1) Доказательство: Рассмотрим очевидные тождества

Формула умножения вероятностей.

Теорема. Вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого события. Доказательство: Рассмотрим схему случаев

Формула полной вероятности.

(1.9.1) Из рисунка видно, что гипотезы и события несовместны, поэтому

Формула вероятностей гипотез (Байеса).

По формуле умножения имеем (1.10.1) откуда

Повторение опытов.

Схема Бернулли.

Пусть производится n независимых опытов, в каждом из которых может появиться некоторое событие с одной и той же вероятностью 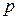. Такой опыт носит название – схема Бернулли. Требуется вычислить вероятность появления события в n опытах m раз. Обозначается такая вероятность – . Рассмотрим сначала пример.

Пример 1.11.1.Производится три выстрела по мишени. Вероятность попадания при каждом выстреле равна 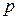. Какова вероятность двух попаданий?

Решение.Обозначим – попадания при первом, втором и третьем выстрелах, 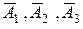– соответственно промахи. Причем

.

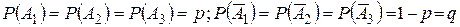Событие 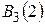– два попадания при трех выстрелах конструируется следующим образом:

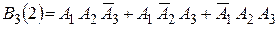
Тогда вероятность .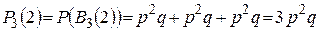

В общем случае конструкция события 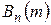выглядит следующим образом

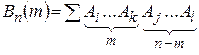. (1.11.1)

Общее число слагаемых равно 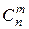(число сочетаний из n по m), поэтому

(1.11.2)

Выражение (9.2) называется – формула Бернулли. Следует обратить внимание на тот факт, что вероятности представляют собой члены разложения бинома . Распределение вероятностей (9.2) называют биномиальным.

Результаты (1.11.1), (1.11.2) можно обобщить на случай, когда событие появляется в каждом опыте со своей вероятностью. В опыте с номером i вероятность появления равна 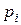, а вероятность не появления равна 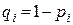. Конструкция события 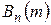усложнится и примет вид

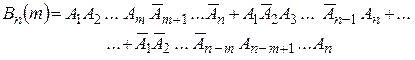(1.11.3)

Формула для вероятности принимает вид

(1.11.4)

Таким образом, в формуле (1.11.4) искомая вероятность равна сумме всевозможных произведений, в которые буквы 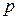с разными индексами входят m раз, а буквы 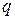с разными индексами входят n-m раз. Для удобного вычисления вероятностей (1.11.4) воспользуемся функцией

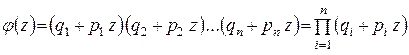(1.11.5)

Легко видеть, что коэффициент при функции (1.11.5) и есть вероятность .

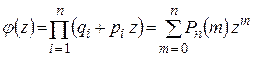(1.11.6)

Многочлен (1.11.5), (1.11.6) называется производящей функцией. В частном случае, когда все вероятности равны 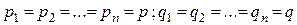, формула (1.11.6) принимает вид

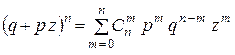(1.11.7)

откуда следует формула (1.11.2).

Если в формулах (1.11.6), (1.11.7) положить 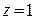, то получим, что сумма всех вероятностей равна единице .

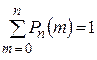Пример 1.11.2.Производится четыре независимых выстрела по мишени с различных расстояний. Вероятности попаданий при этих выстрелах равны 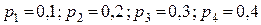. Найти вероятности ни одного, одного, двух, трех и четырех попаданий.

Решение:Составляем производящую функцию:

Таким образом

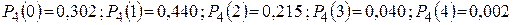
1.11.2. Асимптотическая формула Муавра – Лапласа.

Если число испытаний n в схеме Бернулли велико, то применение на практике формулы Бернулли (1.11.2) становится затруднительным при вычислении факториалов больших чисел.

В таких случаях целесообразно воспользоваться асимптотическими (приближенными) формулами. Одной их таких формул является локальная формула Муавра – Лапласа.

. (1.11.8)

Формула (1.11.8) приближенно рассчитывает вероятность появления события в n опытах раз. Иногда на практике требуется вычислить вероятность того, что число появлений события будет заключено между числам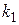и и . Для такого расчета существует интегральная формула Муавра – Лапласа

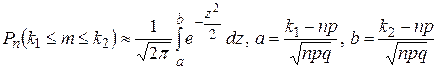. (1.11.9)

Если ввести вспомогательную функцию

, (1.11.10)

то формула (1.11.9) принимает вид

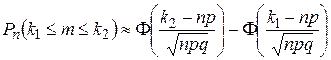. (1.11.11)

Замечание:

Формулы Муавра – Лапласа (1.11.8) – (1.11.11) целесообразно применять при и .

Асимптотическая формула Пуассона.

. (1.11.12) Преобразования в правой части формулы (1.11.12) дают

Случайные дискретные величины.

Случайные величины обозначаются большими латинскими буквами – , а их значения, принимаемые во время опыта малыми – . Знаки отношений между… Пусть в результате опытов случайная величина может принять множество значений… (1.12.1)

Случайные непрерывные величины.

(1.13.1) Соотношение (1.13.1) иногда называют интегральным законом распределения,… Покажем, что с помощью закона (1.13.1) можно определить вероятность попадания на любой заданный отрезок .

Функция плотности вероятности случайной непрерывной величины.

Количество вероятности на единице длины – является средней плотностью… (1.14.1)

Числовые характеристики случайных величин.

Мода случайных величин.

Мода случайной дискретной величины есть ее значение, отвечающее наибольшей вероятности

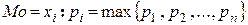(1.15.1)

Мода случайной непрерывной величины есть ее значение, отвечающее локальному максимуму функции плотности вероятности. Различают унимодальные, полимодальные и антимодальные распределения

Квантили случайных величин.

 

Математическое ожидание случайных величин.

(1.15.2) Здесь – частота появления значения . При , величина стремится к некоторому… (1.15.3)

Среднеквадратичное отклонение и дисперсия случайных величин.

. (1.15.6) Из формул (1.15.6) видно, что суммировать просто отклонения нельзя, так как… При , величина стремится к некоторому значению

Моменты случайных величин.

Начальным моментом порядка s случайной дискретной величины X называется величина . (1.15.12) Начальным моментом порядка s случайной непрерывной величины X называется величина

Теоремы о числовых характеристиках случайных величин.

Доказательство:Пусть – неслучайная величина. Тогда формула для ее математического ожидания имеет вид , (1.16.1) что и требовалось доказать.

Законы распределения случайных величин.

Рассмотрим несколько классических законов распределения случайных величин, которые наиболее часто встречаются на практике при решении различного рода задач по теории вероятностей.

Биномиальный закон распределения.

. (1.17.1) Ряд распределения такого закона имеет вид … Отметим основные числовые характеристики этого закона.

Закон распределения Пуассона.

. (1.17.2) Здесь – некоторая положительная величина, которая называется параметром закона… Ряд распределения такого закона имеет вид … m … …

Пример.

На АТС поступают вызовы со средней плотностью 90 вызовов в час. Считая, что число вызовов на любом участке времени распределено по закону Пуассона, найти вероятность того, что за две минуты на станцию поступит ровно 3 вызова.

Решение:

Среднее число вызовов (математическое ожидание) за две минуты равно

.

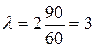По формуле (1.17.2) вероятность поступления ровно 30 вызовов равна

0,224.

Равномерный закон распределения.

. (1.17.3) Интегральная функция распределения для этого закона выражается зависимостью (1.14.3)

Нормальный закон распределения.

. (1.17.5) Интегральная функция распределения для этого закона выражается зависимостью (1.14.3)

Экспоненциальный закон распределения.

Построим закон такого распределения в рамках теории надежности. Пусть некоторое устройство может отказать (выйти из строя) за время некоторое число… . В частном случае, если за время не произойдет ни одного события (устройство не выйдет из строя), то вероятность такого…

Системы случайных величин.

Система двух случайных дискретных величин.

Законом распределения системы случайных дискретных величин называется соотношение , (1.18.1) содержащее полную информацию об этой системе.

Пример 1.18.1.

Проводится два испытания Бернулли с вероятностью успеха 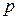и вероятностью неудачи 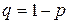. Число успехов в первом испытании – , число успехов во втором испытании – . Случайные величины и могут принимать значения 0 и 1. Построить матрицу распределения для системы случайных дискретных величин .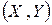

Решение:

Применим формулу Бернулли (1.11.2)

.

,

,

,

.

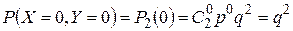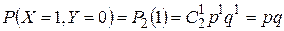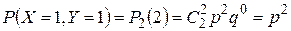Строим таблицу

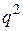
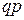
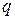
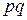
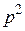
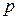
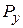
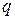
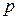
Система двух случайных непрерывных величин.

. (1.18.5) Функцию называют еще двумерной интегральной функцией распределения… Если , то

Условные законы распределения.

. Воспользуемся формулой произведения вероятностей (1.8.2) ,

Числовые характеристики системы двух случайных величин.

. (1.18.21) Центральным моментом порядка системы случайных величин называется… . (1.18.22)

Система нескольких случайных величин.

Пусть система образована совокупностью случайных величин . Функцией распределения этой системы имеет вид

Нормальный закон распределения системы двух случайных величин.

. (1.18.35) Можно показать, что здесь – математические ожидания случайных величин, – их… . (1.18.36)

Предельные теоремы теории вероятностей.

Практика показывает, что наблюдение массы однородных случайных явлений обнаруживает в ней определенные закономерности. Эти закономерности связаны с устойчивостью случайных массовых явлений, при… В этой устойчивости проявляется так называемый закон больших чисел, суть которого заключается в том, что при большом…

Неравенство Чебышева.

. (1.19.1) Доказательство: Пусть для определенности – случайная непрерывная величина, плотность вероятности которой есть . Тогда

Закон больших чисел.

Теорема Чебышева.

, то для любого положительного числа выполняется равенство .

Теорема Бернулли.

Доказательство: Обозначим – число появлений события в независимых испытаниях, – вероятность… .

Центральная предельная теорема.

В таком общем виде центральная предельная теорема была сформулирована советским математиком А. Ляпуновым. На практике замена закона распределения суммы случайных величин нормальным… Рассмотренные нами выше асимптотическая формула Муавра – Лапласа (1.11.8) является следствием центральной предельной…

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.

Основные задачи математической статистики.

Изучая законы распределения случайных величин, мы не затрагивали вопроса о том, откуда берутся, на каком основании устанавливаются эти законы. Разработка методов регистрации, описания и анализа статистических… Задачи математической статистики касаются вопросов обработки наблюдений над случайными массовыми явлениями. В…

Простая статистическая совокупность. Статистическая функция распределения.

называется простым статистическим рядом. Если значения расположены по возрастанию, то такая таблица называется вариационным рядом. Простой статистический ряд представляет собой первичную форму записи… Статистической функцией распределения случайной величины называется частота события в данном статистическом…

Статистический ряд. Гистограмма.

Разделим весь диапазон наблюденных значений на k отрезков, которые называются разрядами и могут иметь неодинаковую длину . Подсчитаем количество значений , приходящееся на каждый –й разряд. Это число разделим на общее число наблюдений и…

Числовые характеристики статистического распределения.

, (2.4.1) есть статистическое среднее случайной величины. Согласно закону больших чисел, при неограниченном увеличении числа опытов статистическое среднее приближается…

Выбор теоретического распределения по методу моментов.

Предположим, что на основании опытных данных о случайной величине известны ее статистический ряд, гистограмма и статистические моменты распределения… , (2.5.1) где – неизвестные параметры.

Пример 2.5.1.

Произведено 500 измерений боковой ошибки наводки при стрельбе с самолета по наземной цели. Результаты измерений (в тысячных долях радиана) сведены в статистический ряд

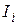
	-4;-3	-3;-2	-2;-1	-1;0	0;1	1;2	2;3	3;4

Требуется:

1. Вычислить относительные частоты боковой ошибки .

2. Выровнять это распределение с помощью нормального закона

.

3. Построить сравнительные диаграммы для функций теоретического и экспериментального распределений и .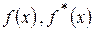

Решение:

Нормальный закон зависит от двух параметров 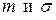. Подберем эти параметры так, чтобы сохранить первые два момента (математическое ожидание и дисперсию статистического распределения).

1. Вычислим сначала относительные частоты боковой ошибки по формуле.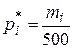

2. Вычислим приближенно статистическое среднее 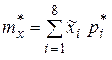ошибки наводки, причем за представителя каждого разряда примем его середину.

3. Для определения дисперсии вычислим сначала второй начальный момент по формуле .

4. Вычислим приближенно дисперсию по формуле и среднеквадратичное отклонение по формуле .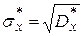

Результаты расчетов сведем в таблицу.

Число опытов
Начало разряда	-4	-3	-2	-1
Конец разряда	-3	-2	-1
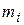
	0,012	0,050	0,144	0,266	0,240	0,176	0,092	0,020
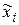
	-3,500	-2,500	-1,500	-0,500	0,500	1,500	2,500	3,500
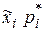
	-0,042	-0,125	-0,216	-0,133	0,120	0,264	0,230	0,070
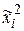
	12,250	6,250	2,250	0,250	0,250	2,250	6,250	12,250
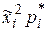
	0,147	0,313	0,324	0,067	0,060	0,396	0,575	0,245
	0,168
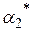
	2,126
	2,098
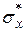
	1,448

Выберем параметры 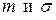нормального закона так, чтобы выполнялись условия 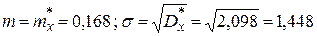. Таким образом .

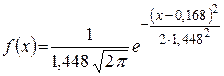Построим теперь сравнительные диаграммы функций распределения и 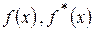. Для этого вычислим значения законов теоретических и экспериментальных распределений в границах разрядов и построим таблицу:

	-4	-3	-2	-1
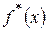
	0,012	0,050	0,144	0,266	0,240	0,176	0,092	0,020	0,000
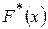
	0,012	0,062	0,206	0,472	0,712	0,888	0,980	1,000	1,000
	0,004	0,025	0,090	0,199	0,274	0,234	0,124	0,041	0,008
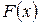
	0,002	0,014	0,067	0,210	0,454	0,717	0,897	0,975	0,996

Для вычисления значений функции 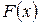следует использовать встроенную функцию EXCEL НОРМРАСП(x;0,168;1,448;ИСТИНА), а для вычисления значений функции – НОРМРАСП(x;0,168;1,448;ЛОЖЬ).

В качестве значений функции следует выбирать частоты , так как все длины разрядов равны единице. Значения функции 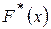вычисляются по формуле .

Диаграммы с графиками этих функций имеют вид

 

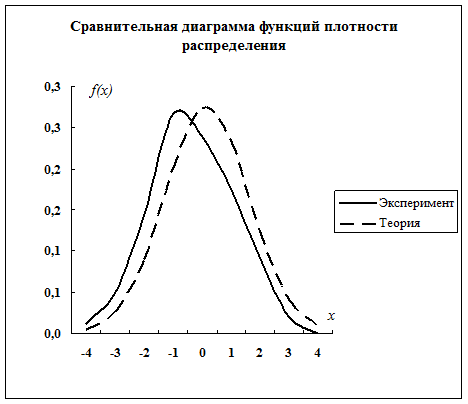
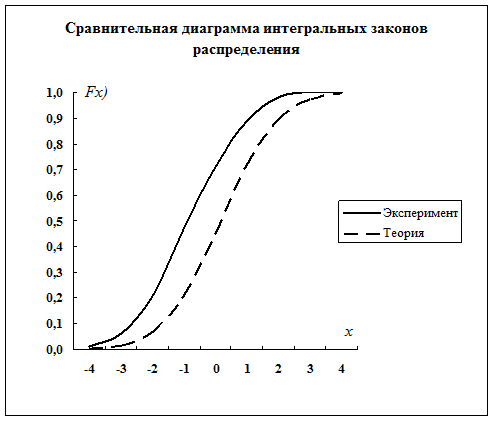
Проверка правдоподобия гипотезы о виде закона распределения.

Идея применения критериев согласия заключается в следующем. Пусть известен эмпирический закон статистического распределения случайной… Для определенности в качестве гипотезы примем факт, что случайная величина имеет теоретическое распределение .

Критерии согласия.

Предположим, что произведено n независимых опытов, в каждом из которых случайная величина приняла определенное значение. Результаты опытов сведены в… Требуется проверить, согласуются ли экспериментальные данные с гипотезой о…

Пример 2.7.1.

Проверим теперь правдоподобие гипотезы о виде закона распределения по критерию согласия Пирсона для примера 2.5.1. Заданное статистическое распределение аппроксимировано теоретической кривой.

Проверим согласованность теоретического и статистического законов распределения:

1. Находим вероятности попадания в разряды по формуле

. (2.7.5)

 

2. Составляем сравнительную таблицу чисел попаданий в разряды 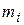и соответствующих значений .

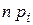3. Вычисляем значение меры расхождения .

4. Определяем число степеней свободы: .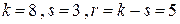

5. Результаты вычислений вносим в таблицу.

Число опытов
Начало разряда	-4	-3	-2	-1
Конец разряда	-3	-2	-1
Число попаданий
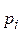
	0,012	0,053	0,143	0,244	0,263	0,180	0,078	0,021
	6,171	26,413	71,387	121,939	131,698	89,942	38,828	10,588
	0,005	0,076	0,005	1,003	1,039	0,042	1,325	0,033
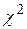
	3,527
Вероятность	0,619

Примечания:

1. Функция 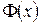– встроена в EXCEL под именем НОРМСТРАСП.

2. Для определения искомой вероятности следует воспользоваться встроенной функцией EXCEL ХИ2РАСП(;).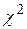

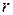Расчет вероятности по таблице дает = 0,619. Эта вероятность малой не является; поэтому гипотезу о том, что величина распределена по нормальному закону, можно считать правдоподобной.

Рассмотрим еще один критерий согласия Колмогорова А.Н.. В качестве меры расхождения между теоретическим и статистическим распределениями в нем принимается максимальное значение модуля разности между статистической функцией распределения 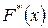и соответствующей теоретической функцией распределения : .

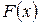Основанием для выбора в качестве меры расхождения величины D является простота ее вычисления. Можно показать, что, какова бы ни была функция распределения 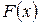случайной непрерывной величины X, при неограниченном возрастании числа независимых наблюдений n вероятность неравенства

стремится к пределу

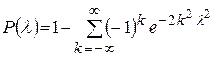
Схема применения критерия Колмогорова А.Н. следующая: строятся статистическая функция распределения 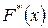и предполагаемая теоретическая функция распределения 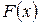, и определяется максимум модуля разности между ними. Далее, определяется величина

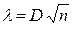
и вычисляется вероятность . Если вероятность весьма мала, гипотезу следует отвергнуть как неправдоподобную; при сравнительно больших значениях ее можно считать совместимой с опытными данными.

Критерий Колмогорова А.Н. своей простотой выгодно отличается от описанного ранее критерия; поэтому его весьма охотно применяют на практике.

Следует, однако, оговорить, что этот критерий можно применять только в случае, когда гипотетическое распределение 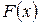полностью известно заранее из каких-либо теоретических соображений, т. е. когда известен не только вид функции распределения 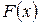, но и все входящие в нее параметры.

Точечные оценки для неизвестных параметров распределения.

Пусть закон распределения случайной величины содержит неизвестный параметр , который необходимо оценить по результатам независимых опытов, в каждом… Обозначим эти значения – и будем рассматривать их как экземпляров случайной… , (2.8.1)

Свойство состоятельности.

При увеличении числа опытов 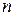величина 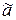должна сходится по вероятности к параметру .

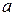Свойство несмещенности.

При использовании величины 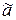вместо 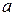не должна накапливаться ошибка в одну или другую сторону

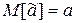(2.8.2)

Свойство эффективности.

Выбранная несмещенная оценка должна обладать наименьшей дисперсией.

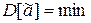(2.8.3)

Величину 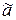, называют иногда точечной оценкой для параметра .

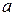Оценки для математического ожидания и дисперсии.

В качестве оценки для математического ожидания возьмем среднее арифметическое опытных значений . (2.9.1) Согласно закону больших чисел эта оценка является состоятельной, при величина по вероятности. Эта же оценка является и…

Доверительный интервал. Доверительная вероятность.