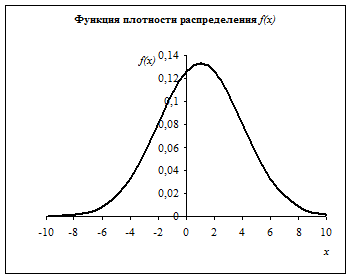
Функция плотности вероятности случайной непрерывной величины.
Пусть 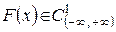 . Рассмотрим точку
. Рассмотрим точку  и дадим ей приращение
и дадим ей приращение 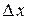 . Вычислим вероятность попадания случайной величины
. Вычислим вероятность попадания случайной величины  на отрезок
на отрезок 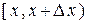 . По формуле (1.13.2) имеем
. По формуле (1.13.2) имеем
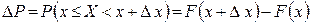
Количество вероятности на единице длины 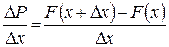 – является средней плотностью вероятности. Если вычислить предел
– является средней плотностью вероятности. Если вычислить предел
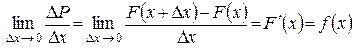 (1.14.1)
(1.14.1)
получим плотность вероятности в точке. Функция  называется функцией плотности вероятности или просто плотностью вероятности.
называется функцией плотности вероятности или просто плотностью вероятности.
Применяя к формуле (11.2) формулу Ньютона – Лейбница, получим новое выражение для вероятности попадания случайной величины на заданный отрезок
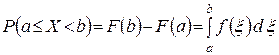 (1.14.2)
(1.14.2)
Величина 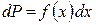 – называется элемент вероятности. Полагая в формуле (1.14.2)
– называется элемент вероятности. Полагая в формуле (1.14.2) 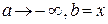 , находим выражение закона распределения через плотность вероятности
, находим выражение закона распределения через плотность вероятности
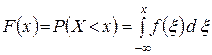 (1.14.3)
(1.14.3)
Из формул (1.14.1) – (1.14.3) и свойств функции распределения 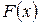 следуют свойства функции плотности распределения
следуют свойства функции плотности распределения  :
:
1) 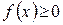 , (так как функция
, (так как функция 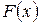 взрастает),
взрастает),
2) 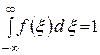 (так как
(так как 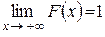 ),
),
3) 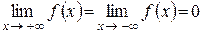 (так как несобственный интеграл сходится).
(так как несобственный интеграл сходится).
С помощью этих свойств можно представить себе общий вид эскиза графика функции распределения  .
.