Среднеквадратичное отклонение и дисперсия случайных величин.
Рассмотрим сначала случайную дискретную величину  . Числовые характеристики мода, медиана, квантили и математическое ожидание характеризуют положение случайной величины
. Числовые характеристики мода, медиана, квантили и математическое ожидание характеризуют положение случайной величины  на оси абсцисс, но не описывают ее рассеивание. Для описания рассеивания случайной величины
на оси абсцисс, но не описывают ее рассеивание. Для описания рассеивания случайной величины  относительно математического ожидания введем отклонения
относительно математического ожидания введем отклонения  . Каждое из таких отклонений в результате
. Каждое из таких отклонений в результате 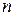 опытов появляется
опытов появляется  раз. Величина
раз. Величина  может быть как положительной, так и отрицательной, поэтому возведем отклонения в минимальную четную степень (в квадрат). Вычислим среднее значение квадратов отклонений и извлечем из него квадратный корень из соображения сохранения размерности
может быть как положительной, так и отрицательной, поэтому возведем отклонения в минимальную четную степень (в квадрат). Вычислим среднее значение квадратов отклонений и извлечем из него квадратный корень из соображения сохранения размерности
 . (1.15.6)
. (1.15.6)
Из формул (1.15.6) видно, что суммировать просто отклонения нельзя, так как положительные и отрицательные значения «гасят» друг друга.
При  , величина
, величина  стремится к некоторому значению
стремится к некоторому значению 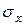
 (1.15.7)
(1.15.7)
Величина (1.15.7) называется среднеквадратичным отклонением случайной величины  , квадрат этой величины
, квадрат этой величины
 (1.15.8)
(1.15.8)
называется дисперсией случайной величины  . Иногда дисперсию и среднеквадратичное отклонение обозначают –
. Иногда дисперсию и среднеквадратичное отклонение обозначают – 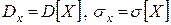 .
.
Если случайная величина  непрерывна, то формула (1.15.8) принимает вид
непрерывна, то формула (1.15.8) принимает вид
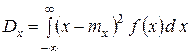 (1.15.9)
(1.15.9)
Из формул (1.15.3), (1.15.4) и (1.15.8), (1.15.9) следует соотношение
 (1.15.10)
(1.15.10)
Здесь  – центрированная случайная величина или флуктуация случайной величины. Из соображений безразмерности иногда рассматривают так называемый коэффициент ковариации
– центрированная случайная величина или флуктуация случайной величины. Из соображений безразмерности иногда рассматривают так называемый коэффициент ковариации
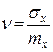 (1.15.11)
(1.15.11)