Теоремы о числовых характеристиках случайных величин.
Теорема 1. Математическое ожидание неслучайной величины равно самой этой величине.
Доказательство:Пусть  – неслучайная величина. Тогда формула для ее математического ожидания имеет вид
– неслучайная величина. Тогда формула для ее математического ожидания имеет вид
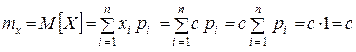 , (1.16.1)
, (1.16.1)
что и требовалось доказать.
Теорема 2. Неслучайный множитель можно выносить за знак математического ожидания.
Доказательство:Пусть 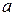 – неслучайный множитель,
– неслучайный множитель,  – случайная величина. Тогда
– случайная величина. Тогда
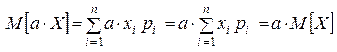 , (1.16.2)
, (1.16.2)
что и требовалось доказать.
Теорема 3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий.
Доказательство:Пусть  – случайные величины. Тогда
– случайные величины. Тогда
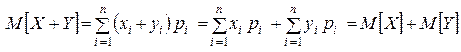 , (1.16.3)
, (1.16.3)
что и требовалось доказать.
Теорема 4. Математическое ожидание от линейной комбинации случайных величин выражается соотношением
 (1.16.4)
(1.16.4)
Доказательство:Автоматически следует их теорем 2, 3.
Теорема 5. Дисперсия неслучайной величины равна нулю.
Доказательство:Пусть  – неслучайная величина. Тогда формула для ее дисперсии имеет вид
– неслучайная величина. Тогда формула для ее дисперсии имеет вид
 , (1.16.5)
, (1.16.5)
что и требовалось доказать.
Теорема 6. При вынесении неслучайного множителя за знак дисперсии, его следует возвести в квадрат.
Доказательство:Пусть 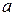 – неслучайный множитель,
– неслучайный множитель,  – случайная величина. Тогда
– случайная величина. Тогда
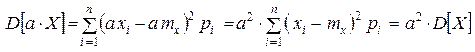 , (1.16.6)
, (1.16.6)
что и требовалось доказать.
Следствие:Для среднеквадратичного отклонения имеет место формула
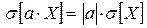 (1.16.7)
(1.16.7)
Теорема 7. Дисперсия суммы двух случайных величин выражается формулой
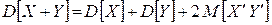 (1.16.8)
(1.16.8)
Доказательство:Пусть  – случайные величины. Тогда с учетом формулы (13.9) имеем
– случайные величины. Тогда с учетом формулы (13.9) имеем
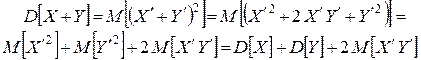 , (1.16.9)
, (1.16.9)
что и требовалось доказать.
Замечание:Величина
 (1.16.10)
(1.16.10)
называется корреляционным моментом случайных величин  .
.
Теорема 8. Дисперсия от линейной комбинации случайных величин выражается соотношением
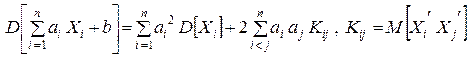 (1.16.11)
(1.16.11)
Доказательство:Автоматически следует их теорем 6, 7.