Экспоненциальный закон распределения.

Экспоненциальное или показательное распределение случайной величины применяется в таких приложениях теории вероятностей, как теория массового обслуживания, теория надежности и т.д.

Построим закон такого распределения в рамках теории надежности. Пусть некоторое устройство может отказать (выйти из строя) за время 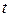некоторое число раз – 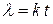. Коэффициент 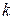называется интенсивностью отказов (среднее число событий, происходящих в единицу времени). Очевидно, что вероятность того, что за время 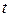произойдет событий, определяется формулой Пуассона (1.11.13)

.

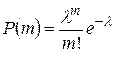В частном случае, если за время 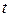не произойдет ни одного события (устройство не выйдет из строя), то вероятность такого события будет равна

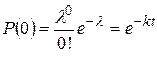. (1.17.10)

Введем случайную величину 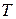– время безотказной работы. Тогда вероятность безотказной работы от момента эксплуатации устройства равна

. (1.17.11)

Функция 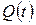называется функцией надежности устройства.

Закон распределения случайной величины 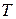задается формулой

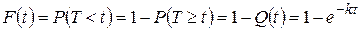. (1.17.12)

Функция плотности вероятности для случайной величины 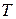вычисляется по формуле

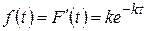. (1.17.13)

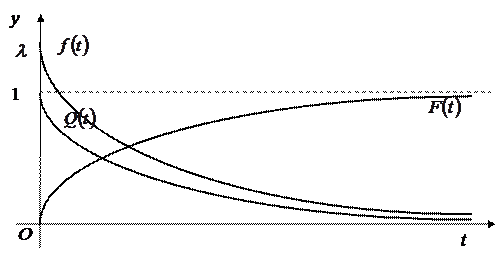
Закон распределения случайной величины 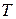с плотностью вероятности (1.17.13) и есть экспоненциальный или показательный закон распределения.

Отметим основные числовые характеристики этого закона.

1. Площадь криволинейной трапеции

.

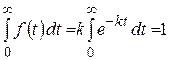2. Математическое ожидание

.

3. Дисперсия

.

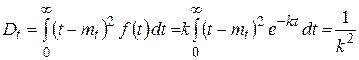4. Среднеквадратичное отклонение

.

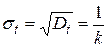5. Коэффициент асимметрии

.

6. Эксцесс

.

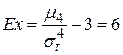Рассмотрим важное свойство экспоненциального закона распределения. Предположим, что на отрезке времени 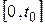не было отказа устройства. Вычислим вероятность отказа этого устройства на промежутке времени 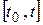. Обозначим события 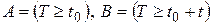. Вероятности этих событий определяются по формуле (1.17.11)

.

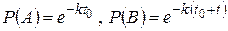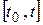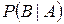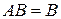В этих обозначениях вероятность отказа устройства на промежутке времени есть условная вероятность события . Для ее нахождения отметим, что произведение событий и имеет вид и

.

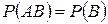С другой стороны, применяя формулу вероятности произведения событий (1.8.1), получаем

.

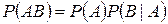Сравнивая полученные формулы, находим

.

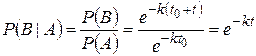Эта формула показывает, что вероятность безотказной работы за предстоящее время 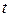не зависит оттого, насколько долго проработало это устройство. Это означает, что устройство при работе не стареет, отказывает внезапно по схеме внезапных повреждений.

1.17.6. Гамма – распределение.

Альтернативой внезапным (мгновенным) повреждениям служат накапливающиеся повреждения, постепенно приводящие к отказу. К таким отказам можно отнести износы шин, подшипников, кинескопов, обуви и т.д.

Износ некоторого устройства можно моделировать монотонно возрастающей функцией 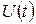, которая описывает процесс накопления повреждений во время эксплуатации. При достижении некоторого порога, некоторого события 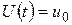, происходит отказ всего устройства. Снова введем случайную величину 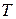– время безотказной работы.

Будем считать, что

1. Средняя скорость износа (накопления элементарных повреждений) постоянна – в единицу времени в среднем будет 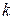повреждений.

2. Количество элементарных повреждений за время 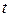подчиняется закону Пуассона с параметром .

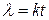3. При накоплении 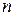элементарных повреждений наступает отказ работы устройства.

Таким образом, накопление повреждений происходит случайными скачками на величину 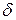. Износ наступает при .

Вероятность иметь элементарных повреждений за время 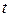находится по формуле Пуассона (1.11.13)

.

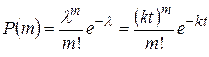Вероятность безотказной работы за время 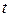– , равна вероятности того, что элементарных повреждений будет меньше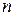

.

Функция распределения такого закона принимает вид

.

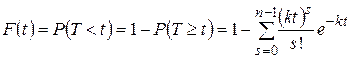Находим функцию плотности вероятности

.

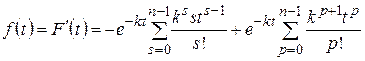В первой сумме отбросим нулевое слагаемое, а во второй сумме заменим индекс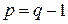

.

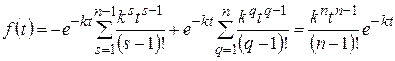Таким образом, плотность вероятности закона распределения выражается формулой

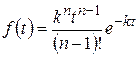. (1.17.14)

Формулу (1.17.14) можно обобщить на случай любых действительных значений 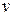. Для этого можно использовать специальную гамма функцию

.

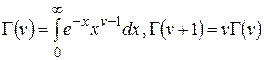Известно, что при натуральных аргументах гамма функция выражает значения факториала

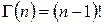
Таким образом, гамма распределение функция плотности вероятности имеет вид

. (1.17.15)

Отметим основные числовые характеристики гамма распределения.

1. Математическое ожидание

.

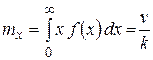3. Дисперсия

.

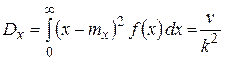4. Среднеквадратичное отклонение

.

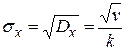5. Коэффициент асимметрии

.

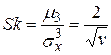6. Эксцесс

.

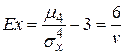Очевидно, что при 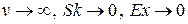. Можно показать, что в пределе получится нормальное распределение.