Система двух случайных непрерывных величин.
Пусть теперь систему образуют две случайные непрерывные величины 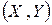 . Законом распределения этой системы называется вероятность события
. Законом распределения этой системы называется вероятность события 
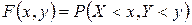 . (1.18.5)
. (1.18.5)
Функцию 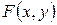 называют еще двумерной интегральной функцией распределения вероятности.
называют еще двумерной интегральной функцией распределения вероятности.
Если 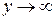 , то
, то
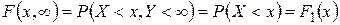 . (1.18.6)
. (1.18.6)
Здесь  – функция распределения случайной величины
– функция распределения случайной величины  .
.
Если  , то
, то
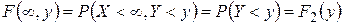 . (1.18.7)
. (1.18.7)
Здесь  – функция распределения случайной величины
– функция распределения случайной величины  .
.
Очевидно, что
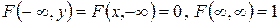 .
.
Вычислим вероятность попадания случайной точки 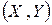 в прямоугольник с вершинами
в прямоугольник с вершинами  .
.
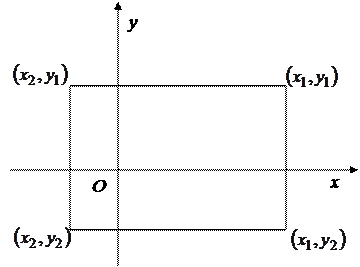
 (1.18.8)
(1.18.8)
Если  , то из формулы (1.18.8) получается известная формула
, то из формулы (1.18.8) получается известная формула
 .
.
Пусть 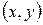 значение системы случайных величин
значение системы случайных величин 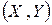 , полученные во время опыта. Дадим приращения
, полученные во время опыта. Дадим приращения  этим значениям. Образуется элементарный прямоугольник.
этим значениям. Образуется элементарный прямоугольник.

Вероятность попадания в этот прямоугольник обозначим 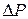 . По формуле (1.18.8) находим
. По формуле (1.18.8) находим
 .
.
Средняя плотность вероятности в этом прямоугольнике выражается формулой
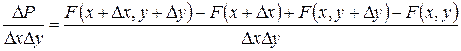 .
.
Переходя к пределу при 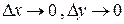 , получаем функцию плотности распределения системы случайных непрерывных величин
, получаем функцию плотности распределения системы случайных непрерывных величин 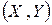
 . (1.18.9)
. (1.18.9)
Поскольку функция 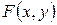 является неубывающей по обоим аргументам, то функция плотности вероятности всегда неотрицательна –
является неубывающей по обоим аргументам, то функция плотности вероятности всегда неотрицательна – 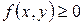 . Можно показать, что
. Можно показать, что
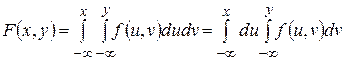 . (1.18.10)
. (1.18.10)
Очевидно, что
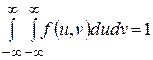 .
.
Законы отдельных величин  и
и  , входящих в систему получаются из формул (1.18.6), (1.18.7) и имеют вид
, входящих в систему получаются из формул (1.18.6), (1.18.7) и имеют вид
 . (1.18.11)
. (1.18.11)
Случайные величины  и
и  называются независимыми, если выполняется соотношение
называются независимыми, если выполняется соотношение
 .
.
Можно показать, что в этом случае будет иметь место подобное соотношение и для функции плотности вероятностей
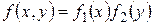 .
.