Условные законы распределения.
Пусть  и
и  зависимые случайные непрерывные величины. Рассмотрим два события
зависимые случайные непрерывные величины. Рассмотрим два события
 .
.
Воспользуемся формулой произведения вероятностей (1.8.2)
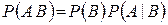 ,
,
или
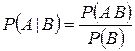 .
.
Подставляя сюда значения событий, получим
 ,
,
или
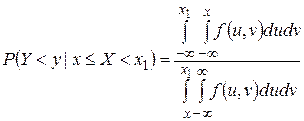 (1.18.12)
(1.18.12)
Переходя в формуле (1.18.12) к пределу при  , используя теорему о среднем значении и вводя обозначение, находим
, используя теорему о среднем значении и вводя обозначение, находим
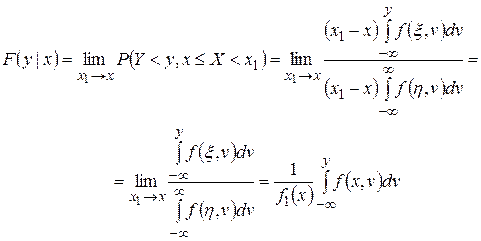 .
.
Здесь принимается во внимание, что  и при
и при  .
.
Функция
 , (1.18.13)
, (1.18.13)
называется условной интегральной функцией распределения случайной величины  при условии
при условии  .
.
Частная производная
 , (1.18.14)
, (1.18.14)
называется условной функцией плотности вероятностей случайной величины  при условии
при условии  .
.
Подставляя формулу (1.18.13) в равенство (1.18.14), получим
 . (1.18.15)
. (1.18.15)
Проинтегрируем соотношение (1.18.15) по всей числовой оси
 .
.
Совершенно аналогично определяются:
Условная интегральная функция распределения случайной величины  при условии.
при условии. 
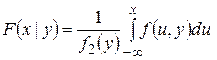 . (1.18.16)
. (1.18.16)
Условная функция плотности вероятностей случайной величины  при условии
при условии  .
.
 . (1.18.17)
. (1.18.17)
Подставляя в последнее из равенств (1.18.11)
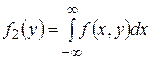
формулу (1.18.15), получаем
 , (1.18.18)
, (1.18.18)
обобщение формулы полной вероятности для случайных величин.
Совершенно аналогично получается вторая симметричная формула полной вероятности
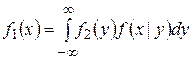 . (1.18.19)
. (1.18.19)
Формулы (1.18.15) и (1.18.17) дают аналоги формулы Байеса для случайных непрерывных величин.
 . (1.18.20)
. (1.18.20)