Числовые характеристики системы двух случайных величин.
Начальным моментом порядка  системы случайных величин
системы случайных величин 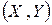 называется математическое ожидание произведения
называется математическое ожидание произведения 
 . (1.18.21)
. (1.18.21)
Центральным моментом порядка  системы случайных величин
системы случайных величин 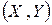 называется математическое ожидание произведения
называется математическое ожидание произведения 
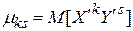 . (1.18.22)
. (1.18.22)
Для случайных дискретных величин формулы (1.18.21), (1.18.22) принимают вид
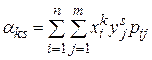 , (1.18.23)
, (1.18.23)
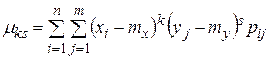 . (1.18.24)
. (1.18.24)
Для случайных непрерывных величин формулы (1.18.21), (1.18.22) принимают вид
 , (1.18.25)
, (1.18.25)
 . (1.18.26)
. (1.18.26)
Рассмотрим частные случаи формул (1.18.21), (1.18.22). Так, например, начальный момент
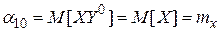 ,
,
есть математическое ожидание случайной величины  , а начальный момент
, а начальный момент
 ,
,
есть математическое ожидание случайной величины  .
.
Центральный момент
 ,
,
есть дисперсия случайной величины  , а центральный момент
, а центральный момент
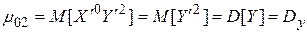 ,
,
есть дисперсия случайной величины  .
.
Центральный смешанный момент

играет в теории вероятностей особую роль и, как было отмечено п. 1.16, называется корреляционным моментом или ковариацией случайных величин.
Для случайных дискретных величин формула для корреляционного момента имеет вид
 . (1.18.27)
. (1.18.27)
Для случайных непрерывных величин формула для корреляционного момента имеет вид
 . (1.18.27)
. (1.18.27)
Корреляционный момент описывает связь между случайными величинами. Так если случайные величины являются независимыми, то он равен нулю. В самом деле, если  , то
, то

Обратное утверждение неверно. Если  , то случайные величины могут быть и зависимыми. В этом случае они называются некоррелированными.
, то случайные величины могут быть и зависимыми. В этом случае они называются некоррелированными.
На практике для оценки связи случайных величин удобнее рассматривать безразмерную величину
 , (1.18.28)
, (1.18.28)
которую называют коэффициентом корреляции.
Коэффициент корреляции для любых случайных величин удовлетворяет неравенству
 . В самом деле, если рассмотреть случайную величину
. В самом деле, если рассмотреть случайную величину  и вычислить по формуле (1.16.9) ее дисперсию
и вычислить по формуле (1.16.9) ее дисперсию

Здесь использовано свойство не отрицательности дисперсии.
Таким образом
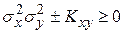 ,
,
откуда
 .
.
Если зависимость между случайными величинами линейна –  , то коэффициент корреляции
, то коэффициент корреляции  . Действительно,
. Действительно,

Дисперсия и среднеквадратичное отклонение величины  равны
равны
 .
.
Таким образом,
 .
.