Нормальный закон распределения системы двух случайных величин.

Рассмотрим систему двух случайных непрерывных величин 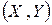. Законом распределения этой системы является нормальный закон распределения, если функция плотности вероятности этой системы имеет вид

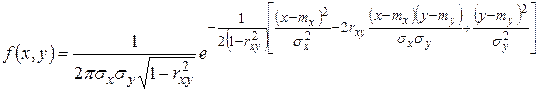. (1.18.35)

Можно показать, что здесь 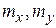– математические ожидания случайных величин, 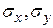– их среднеквадратические отклонения, 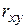– коэффициент корреляции величин 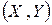. Вычисления по формулам (1.18.31) и (1.18.35) дают

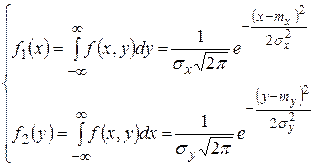. (1.18.36)

Легко видеть, что если случайные величины 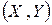, распределенные по нормальному закону не коррелированны , то они являются также и независимыми

.

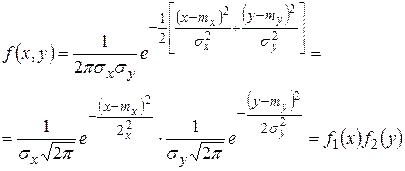Таким образом, для нормального закона распределения не коррелированность и независимость – эквивалентные понятия.

Если 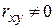, то случайные величины 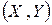зависимы. Условные законы распределения вычисляются по формулам (1.18.20)

. (1.18.37)

Оба закона (1.18.37) представляют собой нормальные распределения. В самом деле, преобразуем, например, второе из соотношений (1.18.37) к виду

.

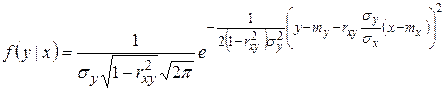Это действительно нормальный закон распределения, у которого условное математическое ожидание равно

, (1.18.38)

а условное среднеквадратичное отклонение выражается формулой

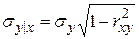. (1.18.39)

Отметим, что в условном законе распределения величины при фиксированном значении от этого значения зависит только условное математическое ожидание, но не условная дисперсия – .

На координатной плоскости зависимость (1.18.38) представляет собой прямую линию

, (1.18.40)

которая называется линией регрессии на .

Совершенно аналогично устанавливается, что условное распределение величины при фиксированном значении

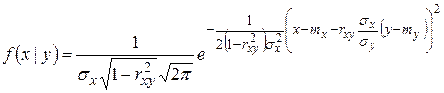, (1.18.41)

есть нормальное распределение с условным математическим ожиданием

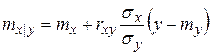, (1.18.42)

условным среднеквадратичным отклонением

. (1.18.43)

В этом случае линия регрессии имеет вид

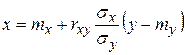. (1.18.44)

Линии регрессии (1.18.40) и (1.18.44) совпадают только тогда, когда зависимость между величинами и является линейной. Если величины и независимы, линии регрессии параллельны координатным осям.