Основные определения
Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию y=f(x), и ее производные 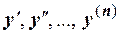 или дифференциалы.
или дифференциалы.
Символически дифференциальное уравнение можно записать так:
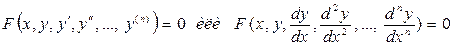 (10.1)
(10.1)
Дифференциальное уравнение называется обыкновенным, если искомая функция y=f(x) зависит от одного независимого переменного.
Если независимых переменных две и больше, то уравнение называется дифференциальным уравнением в частных производных. Мы будем рассматривать обыкновенные дифференциальные уравнения.
Порядком дифференциального уравнения называется порядок наивысшей (старшей) производной, входящей в данное уравнение.
Например,  – обыкновенное дифференциальное уравнение первого порядка;
– обыкновенное дифференциальное уравнение первого порядка; 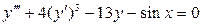 – обыкновенное дифференциальное уравнение третьего порядка;
– обыкновенное дифференциальное уравнение третьего порядка;  – уравнение в частных производных первого порядка.
– уравнение в частных производных первого порядка.
Решением или интегралом дифференциального уравнения называется такая функция y=φ(x), которая, будучи подставлена в уравнение (10.1), обращает его в тождество.
Процесс нахождения решений дифференциального уравнения называется интегрированием этого уравнения.
Общим решением (или общим интегралом) дифференциального уравнения (10.1) называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную y=φ(x, C).
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. На практике частное решение получается из общего не прямым заданием значений произвольных постоянных, а исходя из тех условий, которым должно удовлетворять искомое частное решение. Задание таких условий называется заданием начальных условий, для уравнения 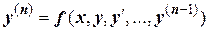 их записывают так
их записывают так
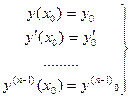 (10.2)
(10.2)
где 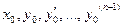 – заданные числа.
– заданные числа.
Для дифференциального уравнения первого порядка начальные условия задают в виде f(x0)=y0 или 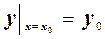 , или у=y0 при х=x0.
, или у=y0 при х=x0.
Задача нахождения частного решения, удовлетворяющего начальным условиям (10.2) называется задачей Коши.
График частного решения дифференциального уравнения называется интегральной кривой. Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.
Среди дифференциальных уравнений встречаются такие, которые имеют решения, не получающиеся из общего решения ни при каких значениях С. Такие решения называются особыми.