Формулы Бернулли, Пуассона и Муавра-Лапласа

Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.

Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p(0<p<1), событие наступит ровно r раз (безразлично, в какой последовательности), равна

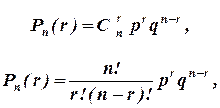
где q=1-p.

Вероятность того, что событие наступит: а) менее rраз; б) более r раз; в) не менее r раз; г) не более r раз – находят соответственно по формулам:

а) P_n(0)+P_n(1)+…+P_n(r-1);

б) P_n(r+1)+P_n(r+2)+…+P_n(n);

в) P_n(r)+P_n(r+1)+…+P_n(n);

г) P_n(0)+P_n(1)+…+P_n(r).

Если число испытаний велико, а вероятность появления события р в каждом испытании очень мала, то пользуются приближенной формулой

,

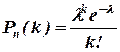где k – число появления события в n независимых испытаниях, l=np (среднее число появления события в n испытаниях) и говорят, что случайная величина распределена по закону Пуассона.

Пример 29. Вероятность рождения мальчика 0.515. В семье 6 детей. Найти вероятность того, что из них:

а) ровно три девочки,

б) не более трех девочек,

в) не менее двух, но не более четырех девочек.

Решение:

а)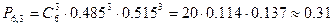

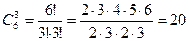
б)

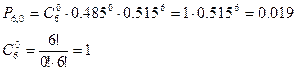
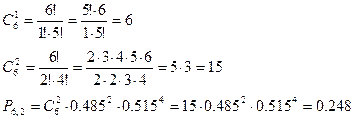
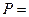
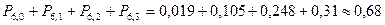
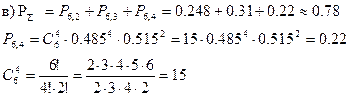
Пример 30. «Средний» человек с вероятностью 3/5 выполняет определенное задание за 1 мин. Предположим, что задание выполнялось 10 людьми. Какова вероятность ровно семи успешных выполнений задания за 1 мин?

Решение. Здесь n = 10, k = 7, р = 3/5. Значит,

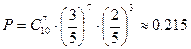
Пример 31. Предположим, что скрещиваются мышь-альбинос и мышь гомозиготного нормального типа (цветная). Какова вероятность двух альбиносов из шести мышей во втором поколении?

Решение. В первом поколении все мыши будут цветными, так как ген альбинизма рецессивен. Легко видеть, что во втором поколении цветными окажутся 3/4 всех мышей. Поскольку все первое поколение имеет тип Сс, скрещивание Сс и Сс с равными вероятностями дает СС, Сс, сС и сс, причем лишь потомство сс является альбиносами. Таким образом, Р (альбинос) = 1/4 и задача сводится к распределению Бернулли при n = 6, k = 2 и р= 1/4. Искомая вероятность есть

 

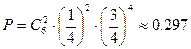
Непосредственное применение формулы Бернулли при большом числе испытаний связано с громоздкими вычислениями, поэтому при больших n используют приближённую формулу Пуассона

Р_n(m)=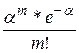, где

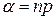
Эту формулу применяют в случае, когда n несколько десятков и более, а произведение np<10 в случае, когда n велико, а np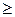10, то формула Пуассона даёт очень грубое приближение, и для расчётов вероятности используют формулу Муавра-Лапласа.

Если число испытаний n достаточно велико (n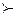100),произведение npq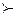20, то вероятность Р_n(m) можно приближенно найти по локальной формуле Муавра-Лапласа

Р_n(m)=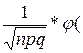х), где 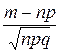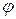х=, (х)=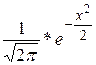– функция Гаусса

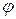(х) – чётная.

В условиях локальной формулы Муавра-Лапласа вероятность того, что число успехов лежит между m₁ и m₂ можно приближенно найти по интегральной формуле Муавра-Лапласа

Р_n(m₁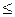m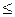m₂)=Ф₀(х₂)–Ф₀(х₁), где х₁=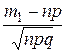, х₂=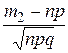, Ф₀(х)=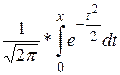– функция Лапласа, Ф₀(х) – нечетная.

Функцию Ф(x) называют функцией Лапласа или интегралом вероятности. Значение интеграла для различных 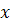вычислены и приведены в таблицах, причем только для 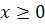. Для нахождения Ф(x) функции для отрицательных значений 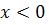пользуются той же таблицей, учитывая, что Ф(x)- нечетная функция, т.е. 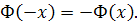Кроме того, в таблице приведены значения лишь до 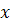=4, так как для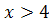можно принять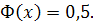

Поэтому вычисление вероятности сводится к расчету 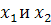и дальнейшему определению по таблице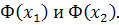

Завод отправил в магазин 5000 ампул с лекарством. Вероятность того, что в пути ампула разобьется, равно 0,0004. Найти вероятность того, что в пути повредится: а) равно 3 ампулы; б) не более 2 ампул.

Решение:

а) Рассматривая транспортировка каждой ампулы как отдельное испытание, можем утверждать, что производится n=5000 повторных испытаний. Пусть событие А – повреждение ампулы в пути . Так как вероятности наступления события А в каждом испытании одинаковы(p=0,0004),то эти испытания независимы. А значит, для вычисления вероятности повреждения в пути равно 3 ампул можно использовать формулу Бернулли:

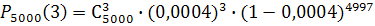
Расчет вероятности по этой формуле достаточно сложен, поэтому воспользуемся приближенной формулой Пуассона. Так как p=0,0004< 0,1 и npq=5000 ·0,0004·0,9994≈2<10, поэтому:

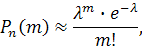
где λ=n·p=5000·0,0004=2 – среднее число появления события А в 5000 испытаний.

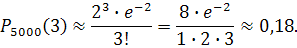
б) Событие (m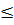2) является суммой трех несовместимых событий (m=0), (m=1) и (m=2).

Следовательно, P(m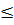2)=P(m=0)+ P(m=1)+ P(m=2)= P₅₀₀₀(0)+P₅₀₀₀(1)+P₅₀₀₀(2)≈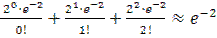(1+2+2)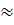0,135·5≈0,677

Пример 33.Средняя плотность болезнетворных микробов в одном м³ воздуха равна 10. Берем на пробу 2 дм³ воздуха. Найти вероятность того, что в них будет обнаружен хотя бы один болезнетворный микроб.

Решение:

1 дм³ = 0,001 м³. 2 дм³ = 0,002 м³.

Вероятность присутствия 1 микроба в 2 дм³: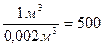

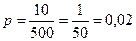
Количество испытаний: 10

Среднее число появлений событий А (1 микроба) в 10 испытаниях: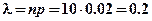

Используем формулу Пуассона

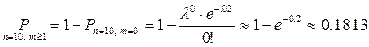
Некоторое редкое заболевание встречается у 0.1% населения. Какова вероятность того, что это заболевание окажется у 4 человек из случайно отобранных 5000 человек?

Решение:

Вероятность заболевания р=0.001. n=5000.

По формуле Пуассона

 

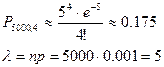
По статистическим данным в среднем 87% новорожденных доживают до 50 лет. Найти вероятность того, что из 1000 новорожденных доля (частость) доживших до 50 лет будет: а) заключена в пределах от 0,9 до 0,95; б) будет отличаться от вероятности этого события не более ,чем на 0,04 (по абсолютной величине).

Решение:

а) вероятность того, что новорожденный доживет до 50 лет, равна 0,87. Т.к. n= 1000 велико (условие npq=1000*0,87*0,13=113,1≥20 выполнено), то используем следствие интегральной теоремы Лапласа. Вначале определим по

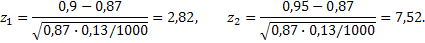
Теперь по формуле

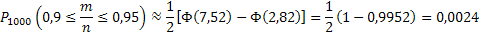
б) По формуле

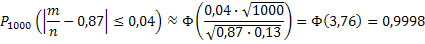
Т. к. неравенство 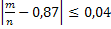равносильно неравенству 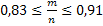, что от 0,83 до 0,91 новорожденных из 1000 доживут до 50 лет.

 

Всхожесть семян оценивается вероятностью 0,8. Найти вероятность того, что из 100 высеянных семян взойдет: а) равно 90; б) от76 до 90 семян.

Решение:

а) Пусть событие А – семя взошло. Рассматривая посев каждого семени как отдельное испытание, можно сказать, что проводится 100 независимых испытаний (в каждом из них событие А наступает с постоянной вероятностью p = p(A) = 0,8). По формуле Бернулли имеем:

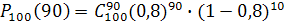
Понятно, что непосредственный расчет по этой формуле окажется трудным. В данной задаче произведение npq равно:

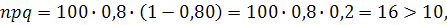
поэтому можно воспользоваться приближенной локальной формулой Лапласа:

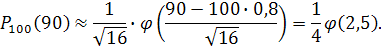
По таблице значений функции 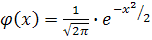найдем: .

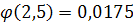Тогда

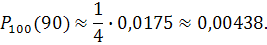
б) Обозначим как (76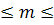90) событие, заключающееся в том, что число m взошедших семян заключено между 76 и 90. Если для вычисления вероятности этого события использовать формулу Бернулли, то придется считать следующую сумму вероятностей:

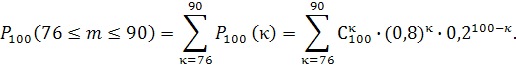
Однако, т.к. np=16>10, то хорошую точность расчета искомой вероятности можно получить при использовании приближенной интегральной формулы Лапласа:

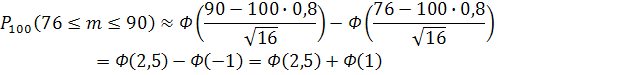
т.к. функция Лапласа нечетная и Ф(–1)=–Ф(1).

По таблице значений Ф(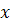) найдем: Ф(2,5)=0,49379; Ф(1)=0,34134.

Тогда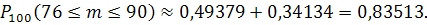

Найдите наиболее вероятное число выигрышей в шахматы в 15 партиях у равносильного противника.

Замечание. Для нахождения наиболее вероятного числа успехов k₀ по заданным n и p можно воспользоваться неравенствами np-q<=k₀<=np+p или правилом: если число np+p не целое, то k₀ равно целой части этого числа; если же np+p целое, то k₀ имеет 2 значения k₀^'=np-q и k₀^''=np+p.

Решение. В этом примере n=15, p=0,5. Число np+p=15*0,5+0,5=7,5+0,5=8.

Ответ: 8 раз.