Нормальный закон распределения

Этот закон наиболее часто встречается на практике. Он является предельным законом, к которому приближаются другие законы распределения. Нормальное распределение является одним из самых важных распределений в статистике. Обычно всё сравнивают с нормальным законом распределения.

Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами µ и σ², если ее плотность вероятности имеет вид:

(см. рис. 12.5а).

Свойства плотности распределения вероятностей:

Она колоколообразная ("колокол Гаусса"), иначе унимодальная.

Плотность определяется двумя параметрами: математическим ожиданием (µ) и средним квадратическим отклонением (σ).

Симметричная относительно среднего.

Среднее и медиана нормального распределения равны.

Кривая сдвигается вправо, если среднее увеличивается при постоянном квадратическом отклонении (рис. 11.56), и сдвигается влево, если среднее уменьшается.

Кривая расширяется, если среднее квадратическое отклонениеσ увеличивается (если среднее постоянно).

Кривая становится более остроконечной с меньшей шириной основания колокола, σ если уменьшается при среднем постоянном (площадь под графиком всегда равна 1) (рис. 11.5в).

Рис. 12.5. Кривая нормального закона распределения и ее изменение при изменении параметров

Дополнительные свойства:

Вероятность того, что нормально распределенная случайная величина X со средним µи средним квадратическим отклонением σ(стандартное отклонение) находится между (µ-σ) и (µ+σ), равна 0,68, т.е. 68% случайной величины X отличается от среднего не более чем на одно стандартное отклонение ± σ(рис. 11.6).

Вероятность того, что нормально распределенная случайная величина X находится между (µ-2σ) и (µ+2σ), равна 0,95, т.е. примерно 95% случайной величины X отличается от среднего на два стандартных отклонения ±2σ (рис.11.6).

Вероятность того, что нормально распределенная случайная величина X находится между (µ-3σ) и (µ+3σ), равна 0,99, т.е. 99% (практически достоверно). Это свойство носит название правило трех сигм (рис. 12.6).

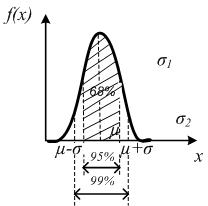
Рис. 12.6. Правило трех сигм

Пример 8.

Построить графики для случая µ₂>µ₁; σ₂>σ₁.

Решение. Рис. 11.5г.