Функции спроса.
Спрос на i-ое благо является функцией от цен и дохода:
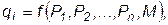 (1)
(1)
где qi – спрос на продукт і;
Р1,Р2,…,Рn – цены на продукты в положении рыночного равновесия;
М – доход потребителей.
Пропорциональное изменение цен и доходов не изменяет спрос, т.е. для любого достаточного числа Р выполняется зависимость:

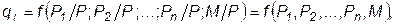 (2)
(2)
где Р – индекс цен.
Коэффициентом эластичности функции (1) называется величина, полученная в результате деления относительного прироста функции на относительный прирост аргумента. Можно вычислять эластичность по ценам и доходам.
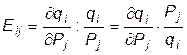 ; i,j = 1,2,…,n . (3)
; i,j = 1,2,…,n . (3)
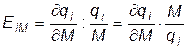 ; i = 1,2,…,n. (4)
; i = 1,2,…,n. (4)
Величины Eij показывают, на сколько процентов изменится спрос на і-ый продукт, если при других неизменных условиях цена на j-ый продукт изменится на 1%. При i=j величины Eij называются коэффициентами эластичности по ценам, если i¹j – перекрестными коэффициентами эластичности.
Эластичность блага, по отношению к собственной цене, является отрицательной величиной (Eii<0), т.е. когда цена на нее увеличивается, то спрос на благо уменьшается. Если Eij<0, то считают, что продукты i и j взаимодополняют друг друга. При Eij>0 продукты i и j взаимозаменяемые; если Eij=0, то продукты i и j независимые.
Между эластичностью по ценам и доходу существует соотношение
 (5)
(5)
Наиболее распространены на практике два типа функций спроса:
линейная 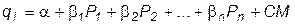 , (6)
, (6)
и показательная или линейно-логарифмическая
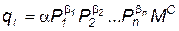 , т.е.
, т.е.
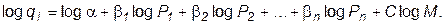 (7)
(7)
В формулах (6), (7) параметры a, b и С являются константами.
Пример 1. Рассмотрим спрос на масло как функцию от цены и дохода потребителей по данным наблюдений за 18 лет.
Таблица 1
Выходные данные примера 1.
| Год | Количество потребления масла на душу населения (кг) | Цена потребителя за 1 кг (условная денежная единица), пересчитанная с учетом индекса цен | Доход на душу населения (условная денежная единица), пересчитанный с учетом индекса цен |
| 5,46 | 3,53 | ||
| 5,73 | 3,64 | ||
| 5,58 | 3,75 | ||
| 5,87 | 3,71 | ||
| 5,12 | 3,74 | ||
| … | … | … | … |
| 5,80 | 3,92 |
Пусть эта функция линейно-логарифмическая (7). Обозначим в уравнении регрессии (7):
Y – логарифм от количества потребления масла;
X1 – логарифм от цены;
X2 – логарифм от дохода;
b1 – эластичность по цене;
b2 – эластичность по доходу;
u – случайная переменная.
 (8)
(8)
Параметры этой зависимости оцениваем методом наименьших квадратов. Воспользуемся упрощенной записью системы нормальных уравнений, которая использует простые и смешанные моменты второго порядка относительно 2-х переменных Xj и Y:
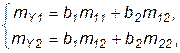 (9)
(9)
где 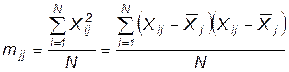 ;
;
 .
.
Вычисленные значения моментов mjj и mYj равны:
mYY=0,00152; mY1=0,00062; mY2=0,00257;
m11=0,00113; m12=0,00323;
m22=0,00996.
Подставим полученные значения в систему (9):
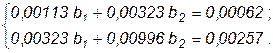
Решение системы найдем методом обратной матрицы. Для упрощения расчетов умножим все коэффициенты на 100.
Матрица системы
 .
.
Обратная матрица
 .
.
Отсюда
 .
.
Постоянный коэффициент а0 рассчитываем при условии, что уравнение регрессии должно пройти через среднее арифметическое всех переменных:
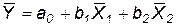 .
.
0,76013 = а0 – (2,58681) × (0,56974) + (1,09693) × (3,05840);
а0 = -1,12091.
Уравнение регрессии имеет такой вид:
Y = -1,12901 – 2,58681X1 + 1,09693X2 .
Этот результат имеет такой смысл: если допущения статистического анализа выполняются, то на каждый процент повышения цены на масло, при всех других неизменных условиях, спрос на масло снизится на 2,6%. Если при тех же условиях существующий доход повысится на 1%, то спрос на масло повысится на 1,1%.
Рассчитаем коэффициент детерминации:
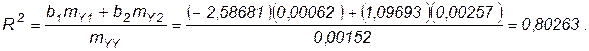
Следовательно 80% дисперсии зависимой переменной Y можно объяснить колебаниями переменных Х1 и Х2.
Для проверки нулевой гипотезы, что ни одна из независимых переменных Х1 и Х2 не связана линейно с зависимой переменной Y, воспользуемся F критерием.
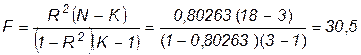 .
.
Табличное значение F, которое отвечает К-1=2 и N-K=5 степеням свободы и уровню табл. существенности 0,95, равно 3,68, т.е. значительно меньше эмпирического. Нулевую гипотезу можно отвергнуть.
Для определения надежности коэффициентов регрессии рассчитаем t –статистики по формуле:
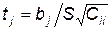 ,
,
где S - стандартная погрешность оценки уравнения:
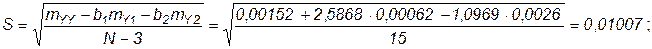
Сii – диагональные коэффициенты обратной матрицы А-1, которая была рассчитана выше.
Для проверки bi вычисляем:
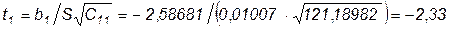 ,
,
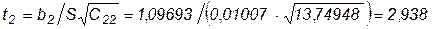 .
.
Величины t1 и t2 имеют распределение Стьюдента с N-K=18-3=15 степенями свободы при уровне значимости 0,95. Их эмпирические значения превышают табличные (2,131), т.е. оценки b1 и b2 значимые. Рассчитаем интервальные оценки для b1 и b2 :
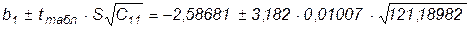 ;
;
доверительный интервал для b1 составляет:
(-6,11441; 0,940079).
Для b2

Отсюда доверительный интервал для b2 (+2,28512; -0,09126).
Введем теперь тенденцию перемены во времени по форме показательной зависимости (Х3 - время); уравнение регрессии будет:
Y = 0,12825 – 2,25498X1 + 0,61624X2 + 0,00912X3.
Этот результат следует понимать так: если при других неизменных условиях (особенно при постоянной прибыли) цена масла повысится на 1%,то спрос на масло уменьшится почти на 2,25%. Если при тех же допущениях (особенно неизменных ценах) повысится на 1%прибыль, то спрос на масло повысится приблизительно на 0,6%.
Коэффициент в уравнении регрессии при Х3 (0,00912) показывает тенденцию. Уравнение регрессии можно потенцианировать
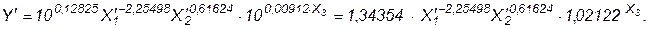
где Y¢, X¢1, X¢2 – антилогарифмы Y, X1, X2.
Тенденция отвечает ежегодному увеличению спроса на масло приблизительно на 2%.
Статистическая проверка показывает, что коэффициент множественной регрессии и индивидуальные коэффициенты регрессии значимы при уровне значимости 0,95.