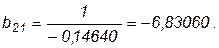Рекурсивные системы.
Особенным случаем однопериодных систем уравнений являются рекурсивные системы. Они позволяют применить МНК к оценке отдельных уравнений системы именно тогда, когда динамическая система представлена в форме однозначной причинной цепи соотношений. Важнейшими допущениями построения рекурсивных систем является их линейность, учет только погрешностей уравнений (погрешности переменных в систему не вносятся). Эти погрешности или отклонения должны быть случайными величинами с нулевым средним значением, постоянным рассеянием и независимыми между собой. Они нормально распределены, не имеют автокорреляции, и корреляция рядов тоже отсутствует.
Пример 4.Известным примером рекурсивных систем является спрос и предложением сельскохозяйственных продуктов, производство которых требует определенного времени. Система имеет вид:
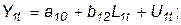 (22)
(22)
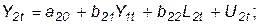 (23)
(23)
Y1t – количество продукта в момент t;
Y2t – цена продукта в момент t;
L1t – цена продукта в момент t;
L2t – любая заранее определенная переменная, например экзогенная переменная прибыли населения в момент t;
U1t, U2t – случайные переменные.
Уравнение (22) – это функция предложения. Оно не должно включать Y2t – цену продукта в тот же момент. На самом деле, количество предложенного сельскохозяйственного продукта зависит не от текущей цены, а, возможно, от Y2,t-1 – цены предыдущего года, когда началось производство этого продукта. L1t – предопределенная переменная.
Второе уравнение (23) – уравнение спроса. Здесь цена в году t (или Y2t) зависит от количества продукта в том же году Y1t. Матрица коэффициентов однопериодных эндогенных переменных Y1t и Y2t – треугольная:
 .
.
Пример 5.Рассмотрим частично динамическую модель, которая состоит из уравнения предложения (пример 2) и уравнения спроса на свинину (пример 6). Если обозначить для года t логарифм количества символом Y1t, а символом Y2t – логарифм цены свинины в t-ом году, то система будет состоять из двух уравнений:
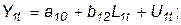 (24)
(24)
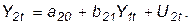 (25)
(25)
Первое уравнение (24) – это уравнение предложения, поскольку для производства свинины необходимо некоторое время, то количество Y1t (эндогенная переменная), предложенное на рынок в году t, зависит не от цены этого года, а от цены предыдущего года L1t.
L1t – предопределенная переменная. Случайная переменная U1t представляет погрешности в этом уравнении и заменяет те переменные, которые должны были бы войти в него, но которыми пренебрегли: показатели затрат, технологические перемены, болезни животных и т.д.
Второе уравнение (25) – это уравнение спроса на свинину. Здесь достигнутая на рынке цена Y2t в году t зависит от предложенного в этом же году количества свинины Y1t. Y1t и Y2t являются эндогенными переменными.
Случайная переменная U2t представляет погрешности в уравнении спроса и заменяет такие не включенные в уравнение переменные, как: погода, цены конкурирующих и заменяющих продуктов, прибыль и т.д.
Система (24)-(25) - рекурсивная и (если пренебречь стохастическими переменными) отображает однозначные причинные зависимости: от цены в этом году посредством уравнения предложения (24) к количеству в следующем году; с помощью уравнения спроса (24); от количества в этом году к соответствующей цене; от этой цены посредством уравнения предложения (24) снова к количеству в следующем году и т.д.
Теперь покажем, что уравнения (24) и (25) идентифицированные. Уравнение (24) не включает одну переменную (Y1t), т.е., по правилу идентификации, на единицу меньше, чем количество эндогенных переменных. Поэтому уравнение (24) точно идентифицировано. Аналогично, точно идентифицировано и уравнение (25).
Если теперь допустить, что случайные переменные U1t и U2t нормально распределены, имеют средние значения, равные нулю, и неизвестные рассеяния  без автокорреляции и корреляции рядов и, кроме того, друг от друга не зависят, то можно использовать МНК для оценки уравнений (24) и (25).
без автокорреляции и корреляции рядов и, кроме того, друг от друга не зависят, то можно использовать МНК для оценки уравнений (24) и (25).
Вычисление уравнения предложения (24) было сделано в примере 2 по данным таблицы 4. Уравнение регрессии имело такой вид:

Коэффициент корреляции R=0,31257, который свидетельствует о слабой связи между Y1t и L1t.
Эмпирическое значение t–статистики равняется 0,806, что ниже табличного значения (tтабл. = 2,447), взятого для уровня существенности 0,95 и N-K=6 степеней свободы. Это свидетельствует о незначимости полученной оценки коэффициента регрессии b12.
Для вычисления функции спроса возьмем данные таблицы 4 из задачи 1. По методу наименьших квадратов:
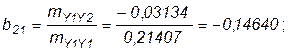
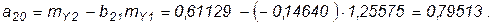
Уравнение регрессии имеет такой окончательный вид:
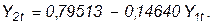
Проверка t–статистики свидетельствует о незначимости коэффициента регрессии (tтабл. > t) для уровня существенности 0,95 и 6 степеней свободы.
Коэффициент регрессии b21 представляет эластичность цены. Чтобы вычислить эластичность спроса, найдем обратное значение b21: