Линейная регрессия.

Пусть составляющие Х и Y двумерной случайной величины (Х, Y) зависимы. Будем считать, что одну из них можно приближенно представить как линейную функцию другой, например

Y ≈ g(Х) = α + βХ, (11.2)

и определим параметры α и β с помощью метода наименьших квадратов.

Определение 11.2. Функция g(Х) = α + βХ называется наилучшим приближениемY в смысле метода наименьших квадратов, если математическое ожидание М(Y - g(Х))² принимает наименьшее возможное значение; функцию g(Х) называют среднеквадратической регрессиейY на Х.

Теорема 11.1. Линейная средняя квадратическая регрессия Y на Х имеет вид:

(11.3)

где - коэффициент корреляции Х и Y.

Доказательство. Рассмотрим функцию

F(α, β) = M(Y – α – βX)² (11.4)

и преобразуем ее, учитывая соот-ношения M(X – m_x) = M(Y – m_y) = 0, M((X – m_x)(Y – m_y)) = =K_xy = rσ_xσ_y:

.

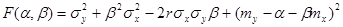Найдем стационарные точки полученной функции, решив систему

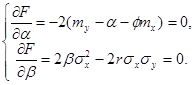Решением системы будет .

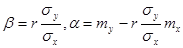Можно проверить, что при этих значениях функция F(α, β) имеет минимум, что доказывает утверждение теоремы.

Определение 11.3. Коэффициент 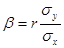называется коэффициентом регрессии Y на Х, а прямая 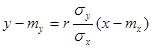- (11.5)

- прямой среднеквадратической регрессии Y на Х.

Подставив координаты стационарной точки в равенство (11.4), можно найти минимальное значение функции F(α, β), равное 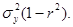Эта величина называется остаточной дисперсией Y относительно Х и характеризует величину ошибки, допускаемой при замене Y на g(Х) = α+βХ. При 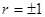остаточная дисперсия равна 0, то есть равенство (11.2) является не приближенным, а точным. Следовательно, при 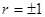Y и Х связаны линейной функциональной зависимостью. Аналогично можно получить прямую среднеквадратической регрессии Х на Y:

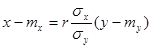(11.6)

и остаточную дисперсию Х относительно Y. При 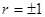обе прямые регрессии совпадают. Решив систему из уравнений (11.5) и (11.6), можно найти точку пересечения прямых регрессии – точку с координатами (т_х, т_у), называемую центром совместного распределения величин Х и Y.