Способы построения оценок.

1. Метод наибольшего правдоподобия.

 

Пусть Х – дискретная случайная величина, которая в результате п испытаний приняла значения х₁, х₂, …, х_п. Предположим, что нам известен закон распределения этой величины, определяемый параметром Θ, но неизвестно численное значение этого параметра. Найдем его точечную оценку.

Пусть р(х_i, Θ) – вероятность того, что в результате испытания величина Х примет значение х_i. Назовем функцией правдоподобия дискретной случайной величины Х функцию аргумента Θ, определяемую по формуле:

L (х₁, х₂, …, х_п; Θ) = p(x₁,Θ)p(x₂,Θ)…p(x_n,Θ).

Тогда в качестве точечной оценки параметра Θ принимают такое его значение Θ* = Θ(х₁, х₂, …, х_п), при котором функция правдоподобия достигает максимума. Оценку Θ* называют оценкой наибольшего правдоподобия.

Поскольку функции L и lnL достигают максимума при одном и том же значении Θ, удобнее искать максимум ln L – логарифмической функции правдоподобия. Для этого нужно:

1) найти производную ;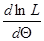

2) приравнять ее нулю (получим так называемое уравнение правдоподобия) и найти критическую точку;

3) найти вторую производную 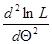; если она отрицательна в критической точке, то это – точка максимума.

Достоинства метода наибольшего правдоподобия: полученные оценки состоятельны (хотя могут быть смещенными), распределены асимптотически нормально при больших значениях п и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками; если для оцениваемого параметра Θ существует эффективная оценка Θ*, то уравнение правдоподобия имеет единственное решение Θ*; метод наиболее полно использует данные выборки и поэтому особенно полезен в случае малых выборок.

Недостаток метода наибольшего правдоподобия: сложность вычислений.

 

Для непрерывной случайной величины с известным видом плотности распределения f(x) и неизвестным параметром Θ функция правдоподобия имеет вид:

L (х₁, х₂, …, х_п; Θ) = f(x₁,Θ)f(x₂,Θ)…f(x_n,Θ).

Оценка наибольшего правдоподобия неизвестного параметра проводится так же, как для дискретной случайной величины.

 

2. Метод моментов.

 

Метод моментов основан на том, что начальные и центральные эмпирические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов, поэтому можно приравнять теоретические моменты соответствующим эмпирическим моментам того же порядка.

Если задан вид плотности распределения f(x, Θ), определяемой одним неизвестным параметром Θ, то для оценки этого параметра достаточно иметь одно уравнение. Например, можно приравнять начальные моменты первого порядка:

,

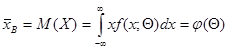получив тем самым уравнение для определения Θ. Его решение Θ* будет точечной оценкой параметра, которая является функцией от выборочного среднего и, следовательно, и от вариант выборки:

Θ = ψ (х₁, х₂, …, х_п).

Если известный вид плотности распределения f(x, Θ₁, Θ₂ ) определяется двумя неизвестными параметрами Θ₁ и Θ₂, то требуется составить два уравнения, например

ν₁ = М₁, μ₂ = т₂.

Отсюда 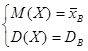- система двух уравнений с двумя неизвестными Θ₁ и Θ₂. Ее решениями будут точечные оценки Θ₁* и Θ₂* - функции вариант выборки:

Θ₁ = ψ₁ (х₁, х₂, …, х_п),

Θ₂ = ψ₂(х₁, х₂, …, х_п).

 

3. Метод наименьших квадратов.

 

 

Если требуется оценить зависимость величин у и х, причем известен вид связывающей их функции, но неизвестны значения входящих в нее коэффициентов, их величины можно оценить по имеющейся выборке с помощью метода наименьших квадратов. Для этого функция у = φ (х) выбирается так, чтобы сумма квадратов отклонений наблюдаемых значений у₁, у₂,…, у_п от φ(х_i) была минимальной:

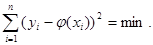
При этом требуется найти стационарную точку функции φ(x; a, b, c…), то есть решить систему:

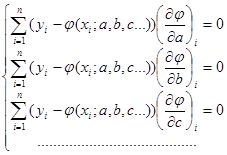
(решение, конечно, возможно только в случае, когда известен конкретный вид функции φ).

Рассмотрим в качестве примера подбор параметров линейной функции методом наименьших квадратов.

Для того, чтобы оценить параметры а и b в функции y = ax + b, найдем 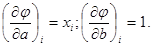Тогда . Отсюда 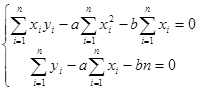. Разделив оба полученных уравнения на п и вспомнив определения эмпирических моментов, можно получить выражения для а и b в виде:

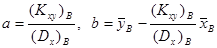. Следовательно, связь между х и у можно задать в виде:

 

4. Байесовский подход к получению оценок.

 

Пусть (Y, X) – случайный вектор, для которого известна плотность р(у|x) условного распреде-ления Y при каждом значении Х = х. Если в результате эксперимента получены лишь значения Y, а соответствующие значения Х неизвестны, то для оценки некоторой заданной функции φ(х) в качестве ее приближенного значения предлагается искать условное математическое ожидание М ( φ‌‌(х)‌‌‌‌‌‌|Y), вычисляемое по формуле:

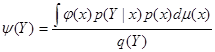, где , р(х) – плотность безусловного распределения Х, q(y) – плотность безусловного распределения Y. Задача может быть решена только тогда, когда известна р(х). Иногда, однако, удается построить состоятельную оценку для q(y), зависящую только от полученных в выборке значений Y.