Закон больших чисел. Неравенство Чебышева. Теоремы Чебышева и Бернулли

Лекция 13.

Закон больших чисел. Неравенство Чебышева. Теоремы Чебышева и Бернулли.

 

Неравенство Чебышева.

  Теорема 13.1(неравенство Чебышева). p( | X – M(X)| < ε ) ≥ D(X)… Доказательство. Пусть Х задается рядом распределения Х х1 х2 … хп р …

Теоремы Чебышева и Бернулли.

будет сколь угодно близка к 1, если число случайных величин достаточно… Замечание. Иначе говоря, при выполнении этих условий

Теорема Бернулли.

(13.2) Доказательство. Введем случайные величины Х1, Х2, …, Хп, где Xi – число… .

Лекция 14.

Центральная предельная теорема Ляпунова. Предельная теорема Муавра-Лапласа.

  Характеристические функции. Для доказательства центральной предельной теоремы используется метод характеристичес-ких функций.

Лекция 15.

Основные понятия математической статистики. Генеральная совокупность и выборка. Вариационный ряд, статистический ряд. Группированная выборка. Группированный статистический ряд. Полигон частот. Выборочная функция распределения и гистограмма.

Математическая статистика занимается установлением закономерностей, которым подчинены массовые случайные явления, на основе обработки статистических данных, полученных в результате наблюдений. Двумя основными задачами математической статистики являются:

- определение способов сбора и группировки этих статистических данных;

- разработка методов анализа полученных данных в зависимости от целей исследования, к которым относятся:

а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости от других случайных величин и т.д.;

б) проверка статистических гипотез о виде неизвестного распределения или о значениях параметров известного распределения.

Для решения этих задач необходимо выбрать из большой совокупности однородных объектов ограниченное количество объектов, по результатам изучения которых можно сделать прогноз относительно исследуемого признака этих объектов.

Определим основные понятия математической статистики.

Генеральная совокупность – все множество имеющихся объектов.

Выборка – набор объектов, случайно отобранных из генеральной совокупности.

Объем генеральной совокупности N и объем выборки n – число объектов в рассматривае-мой совокупности.

Виды выборки:

Повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность;

Бесповторная – отобранный объект в генеральную совокупность не возвращается.

 

Замечание. Для того, чтобы по исследованию выборки можно было сделать выводы о поведе-нии интересующего нас признака генеральной совокупности, нужно, чтобы выборка правиль-но представляла пропорции генеральной совокупности, то есть была репрезентативной(представительной). Учитывая закон больших чисел, можно утверждать, что это условие выполняется, если каждый объект выбран случайно, причем для любого объекта вероятность попасть в выборку одинакова.

 

Первичная обработка результатов.

Пусть интересующая нас случайная величина Х принимает в выборке значение х₁ п₁ раз, х₂ – п₂ раз, …, х_к – п_к раз, причем 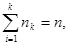где п – объем выборки. Тогда наблюдаемые значения случайной величины х₁, х₂,…, х_к называют вариантами, а п₁, п₂,…, п_к – частотами. Если разделить каждую частоту на объем выборки, то получим относительные частоты Последовательность вариант, записанных в порядке возрастания, называют вариационнымрядом, а перечень вариант и соответствующих им частот или относительных частот – стати-стическим рядом:

xi	x1	x2	…	xk
ni	n1	n2	…	nk
wi	w1	w2	…	wk

 

Пример.

При проведении 20 серий из 10 бросков игральной кости число выпадений шести очков оказалось равным 1,1,4,0,1,2,1,2,2,0,5,3,3,1,0,2,2,3,4,1.Составим вариационный ряд: 0,1,2,3,4,5. Статистический ряд для абсолютных и относительных частот имеет вид:

xi
ni
wi	0,15	0,3	0,25	0,15	0,1	0,05

 

Если исследуется некоторый непрерывный признак, то вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку. Для ее получения интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько равных частичных интервалов длиной h, а затем находят для каждого частичного интервала n_i – сумму частот вариант, попавших в i-й интервал. Составленная по этим результатам таблица называется группированным статистическим рядом:

Номера интервалов			…	k
Границы интервалов	(a, a + h)	(a + h, a + 2h)	…	(b – h, b)
Сумма частот вариант, попав- ших в интервал	n1	n2	…	nk

 

 

Полигон частот. Выборочная функция распределения и гистограмма.

По аналогии с функцией распределения случайной величины можно задать некоторую функцию, относительную частоту события X < x. Определение 15.1. Выборочной (эмпирической) функцией распределения называют… , (15.1)

Лекция 16.

Числовые характеристики статистического распределения: выборочное среднее, оценки дисперсии, оценки моды и медианы, оценки начальных и центральных моментов. Статистическое описание и вычисление оценок параметров двумерного случайного вектора.

Одна из задач математической статистики: по имеющейся выборке оценить значения числовых характеристик исследуемой случайной величины.

Определение 16.1. Выборочным среднимназывается среднее арифметическое значений случайной величины, принимаемых в выборке:

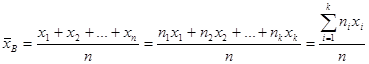, (16.1)

где x_i – варианты, n_i - частоты.

Замечание. Выборочное среднее служит для оценки математического ожидания исследуемой случайной величины. В дальнейшем будет рассмотрен вопрос, насколько точной является такая оценка.

Определение 16.2. Выборочной дисперсией называется

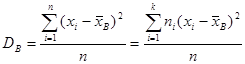, (16.2)

а выборочным средним квадратическим отклонением–

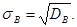(16.3)

Так же, как в теории случайных величин, можно доказать, что справедлива следующая формула для вычисления выборочной дисперсии:

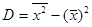. (16.4)

Пример 1. Найдем числовые характеристики выборки, заданной статистическим рядом

xi
ni

 

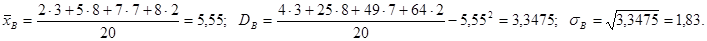Другими характеристиками вариационного ряда являются:

- мода М₀ – варианта, имеющая наибольшую частоту (в предыдущем примере М₀ = 5 ).

- медиана т_е - варианта, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно ( n = 2k + 1 ), то m_e = x_k+1, а при четном n =2k . В частности, в примере 1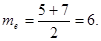

Оценки начальных и центральных моментов (так называемые эмпирические моменты) определяются аналогично соответствующим теоретическим моментам:

- начальным эмпирическим моментом порядка k называется

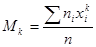. (16.5)

В частности, 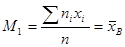, то есть начальный эмпирический момент первого порядка равен выборочному среднему.

- центральным эмпирическим моментом порядка k называется

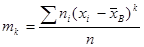. (16.6)

В частности, 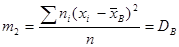, то есть центральный эмпирический момент второго порядка равен выборочной дисперсии.

 

Статистическое описание и вычисление характеристик

Двумерного случайного вектора.

При статистическом исследовании двумерных случайных величин основной задачей является обычно выявление связи между составляющими. Двумерная выборка представляет собой набор значений случайного вектора: (х1,… Если существует зависимость между составляющими двумерной случайной величины, она может иметь разный вид:…

Лекция 17.

Основные свойства статистических характеристик параметров распределения: несме-щенность, состоятельность, эффективность. Несмещенность и состоятельность выборочного среднего как оценки математического ожидания. Смещенность выборочной дисперсии. Пример несмещенной оценки дисперсии. Асимптотически несмещенные оценки. Способы построения оценок: метод наибольшего правдоподобия, метод момен-тов, метод квантили, метод наименьших квадратов, байесовский подход к получению оценок.

Получив статистические оценки параметров распределения (выборочное среднее, выбороч-ную дисперсию и т.д.), нужно убедиться, что они в достаточной степени служат приближе-нием соответствующих характеристик генеральной совокупности. Определим требования, которые должны при этом выполняться.

Пусть Θ* - статистическая оценка неизвестного параметра Θ теоретического распределения. Извлечем из генеральной совокупности несколько выборок одного и того же объема п и вычислим для каждой из них оценку параметра Θ: Тогда оценку Θ* можно рассматривать как случайную величину, принимающую возможные значения Если математическое ожидание Θ* не равно оцениваемому параметру, мы будем получать при вычислении оценок систематические ошибки одного знака (с избытком, если М( Θ*) >Θ, и с недостатком, если М(Θ*) < Θ). Следовательно, необходимым условием отсутствия систе-матических ошибок является требование М(Θ*) = Θ.

 

Определение 17.2. Статистическая оценка Θ* называется несмещенной, если ее математичес-кое ожидание равно оцениваемому параметруΘ при любом объеме выборки:

М(Θ*) = Θ. (17.1)

Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Однако несмещенность не является достаточным условием хорошего приближения к истин-ному значению оцениваемого параметра. Если при этом возможные значения Θ* могут значительно отклоняться от среднего значения, то есть дисперсия Θ* велика, то значение, найденное по данным одной выборки, может значительно отличаться от оцениваемого параметра. Следовательно, требуется наложить ограничения на дисперсию.

 

Определение 17.2. Статистическая оценка называется эффективной, если она при заданном объеме выборки п имеет наименьшую возможную дисперсию.

 

При рассмотрении выборок большого объема к статистическим оценкам предъявляется еще и требование состоятельности.

 

Определение 17.3. Состоятельной называется статистическая оценка, которая при п→∞ стре-мится по вероятности к оцениваемому параметру (если эта оценка несмещенная, то она будет состоятельной, если при п→∞ ее дисперсия стремится к 0).

 

Убедимся, что 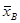представляет собой несмещенную оценку математического ожидания М(Х).

Будем рассматривать 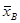как случайную величину, а х₁, х₂,…, х_п, то есть значения исследуемой случайной величины, составляющие выборку, – как независимые, одинаково распределенные случайные величины Х₁, Х₂,…, Х_п, имеющие математическое ожидание а. Из свойств математического ожидания следует, что

Но, поскольку каждая из величин Х₁, Х₂,…, Х_п имеет такое же распределение, что и генеральная совокупность, а = М(Х), то есть М() = М(Х), что и требовалось доказать. Выборочное среднее является не только несмещенной, но и состоятельной оценкой математического ожидания. Если предположить, что Х₁, Х₂,…, Х_п имеют ограниченные дисперсии, то из теоремы Чебышева следует, что их среднее арифметическое, то есть , при увеличении п стремится по вероятности к математическому ожиданию а каждой их величин, то есть к М(Х). Следовательно, выборочное среднее есть состоятельная оценка математического ожидания.

В отличие от выборочного среднего, выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности. Можно доказать, что

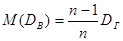, (17.2)

где D_Г – истинное значение дисперсии генеральной совокупности. Можно предложить другую оценку дисперсии – исправленную дисперсию s², вычисляемую по формуле

. (17.3)

Такая оценка будет являться несмещенной. Ей соответствует исправленное среднее квадратическое отклонение

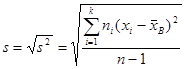. (17.4)

Определение 17.4. Оценка некоторого признака называется асимптотически несмещенной, если для выборки х₁, х₂, …, х_п

, (17.5)

где Х – истинное значение исследуемой величины.

 

Способы построения оценок.

  Пусть Х – дискретная случайная величина, которая в результате п испытаний… Пусть р(хi, Θ) – вероятность того, что в результате испытания величина Х примет значение хi. Назовем функцией…

Лекция 18.

Интервальное оценивание неизвестных параметров. Точность оценки, доверительная вероятность (надежность), доверительный интервал. Построение доверительных интервалов для оценки математического ожидания нормального распределения при известной и при неизвестной дисперсии. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения.

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. Поэтому в таком случае лучше пользоваться интервальными оценками, то есть указывать интервал, в который с заданной вероятностью попадает истинное значение оцениваемого параметра. Разумеется, чем меньше длина этого интервала, тем точнее оценка параметра. Поэтому, если для оценки Θ* некоторого параметра Θ справедливо неравенство | Θ* - Θ | < δ, число δ > 0 характеризует точность оценки( чем меньше δ, тем точнее оценка). Но статистические методы позволяют говорить только о том, что это неравенство выполняется с некоторой вероятностью.

Определение 18.1. Надежностью (доверительной вероятностью) оценки Θ* параметра Θ называется вероятность γ того, что выполняется неравенство | Θ* - Θ | < δ. Если заменить это неравенство двойным неравенством – δ < Θ* - Θ < δ, то получим:

p ( Θ* - δ < Θ < Θ* + δ ) = γ.

Таким образом, γ есть вероятность того, что Θ попадает в интервал ( Θ* - δ, Θ* + δ).

Определение 18.2. Доверительнымназывается интервал, в который попадает неизвестный параметр с заданной надежностью γ.

 

Построение доверительных интервалов.

1. Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии. Пусть исследуемая случайная величина Х распределена по нормальному закону с… р () = 2Ф. Тогда , с учетом того, что , р () = 2Ф=