Доказательство.
Лемма. Пусть 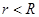 . Тогда
. Тогда 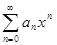 сходится на множестве
сходится на множестве 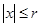 абсолютно и равномерно.
абсолютно и равномерно.
Доказательство. Так как 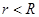 , ряд
, ряд  сходится. Так как
сходится. Так как  , можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
, можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
Замечание. Лемма отнюдь не утверждает равномерной сходимости степенного ряда на  . Да это, вообще говоря, и неверно. Например, прогрессия
. Да это, вообще говоря, и неверно. Например, прогрессия 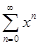 сходится на
сходится на  неравномерно. Однако этот ряд сходится равномерно на любом
неравномерно. Однако этот ряд сходится равномерно на любом 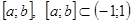 .
.
Пусть теперь 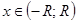 , т.е.
, т.е. 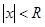 . Выберем
. Выберем  так, чтобы
так, чтобы  . Тогда, по доказанной лемме, ряд сходится на
. Тогда, по доказанной лемме, ряд сходится на 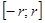 абсолютно и равномерно. Поскольку все функции
абсолютно и равномерно. Поскольку все функции  - непрерывные, сумма ряда есть непрерывная на
- непрерывные, сумма ряда есть непрерывная на 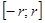 функция. Значит, эта функция непрерывна и в выбранной, произвольной точке
функция. Значит, эта функция непрерывна и в выбранной, произвольной точке  интервала
интервала  .
.
Следствие. (Единственность степенного ряда). Пусть  ,
,  и в некоторой окрестности
и в некоторой окрестности  . Тогда
. Тогда  .
.
Доказательство. При  получаем:
получаем: 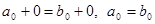 . Поэтому
. Поэтому 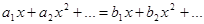 . При
. При  . В правой и левой частях стоят степенные ряды, а они, по-доказанному, есть непрерывные функции, поэтому равенство сохраняется при
. В правой и левой частях стоят степенные ряды, а они, по-доказанному, есть непрерывные функции, поэтому равенство сохраняется при  , откуда
, откуда 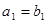 и т.д. (Отметим, что здесь существенно использована непрерывность ряда в точке
и т.д. (Отметим, что здесь существенно использована непрерывность ряда в точке  ).
).
Сформулируем без доказательства еще одну важную теорему.
Теорема. (Абель). Если ряд 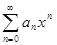 , имеющий сумму
, имеющий сумму 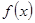 , сходится (хотя бы неабсолютно) при
, сходится (хотя бы неабсолютно) при 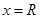 , то
, то  (т.е. сумма ряда непрерывна слева).
(т.е. сумма ряда непрерывна слева).
Теорема. Для любого 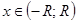
 .
.
Доказательство. Пусть  удовлетворяет неравенствам
удовлетворяет неравенствам  . Тогда степенной ряд сходится равномерно на
. Тогда степенной ряд сходится равномерно на 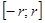 и его можно почленно проинтегрировать. Кроме того,
и его можно почленно проинтегрировать. Кроме того,  . Теорема доказана.
. Теорема доказана.
Теорема. Для любого 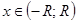
 .
.
Доказательство. Выберем 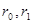 так, чтобы
так, чтобы 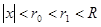 . По определению
. По определению 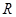 , ряд
, ряд 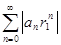 сходится. Поэтому
сходится. Поэтому 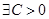 (см. доказательство теоремы 1):
(см. доказательство теоремы 1):  . Рассмотрим величину
. Рассмотрим величину 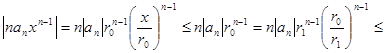
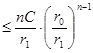 . По признаку Даламбера, ряд
. По признаку Даламбера, ряд  сходится, т.к.
сходится, т.к.  . Значит, мы оценили члены ряда
. Значит, мы оценили члены ряда  при
при 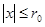 членами сходящегося ряда
членами сходящегося ряда  . Применяя теорему Вейерштрасса на
. Применяя теорему Вейерштрасса на 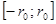 , получаем, что этот ряд равномерно сходится. Следовательно, почленное дифференцирование обосновано на отрезке
, получаем, что этот ряд равномерно сходится. Следовательно, почленное дифференцирование обосновано на отрезке 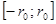 , а значит, и в точке
, а значит, и в точке  . Ввиду произвольности точки
. Ввиду произвольности точки 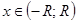 , теорема доказана.
, теорема доказана.
Важное замечание. Из доказанных теорем вытекает, что при интегрировании и дифференцировании радиус сходимости не уменьшается. Но увеличиться он также не может. Если бы, например, он увеличился и стал равен 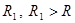 при интегрировании, мы продифференцировали бы этот полученный при интегрировании ряд и получили бы с одной стороны, ряд, совпадающий с исходным, а с другой стороны, имеющий радиус сходимости не меньший, чем
при интегрировании, мы продифференцировали бы этот полученный при интегрировании ряд и получили бы с одной стороны, ряд, совпадающий с исходным, а с другой стороны, имеющий радиус сходимости не меньший, чем  (по доказанному).
(по доказанному).
Итак, радиус сходимости степенного ряда не меняется при почленном интегрировании и дифференцировании.
Однако поведение в концевых точках 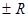 может меняться. Например, ряд
может меняться. Например, ряд  сходится на
сходится на 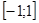 . При этом ряд
. При этом ряд 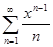 , получающийся из исходного дифференцированием, сходится только на
, получающийся из исходного дифференцированием, сходится только на  , а прогрессия
, а прогрессия 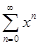 , получающаяся при дифференцировании ряда
, получающаяся при дифференцировании ряда 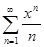 (сходящегося на
(сходящегося на  ), сходится на
), сходится на  .
.
Рассмотрим теперь функцию 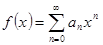 , представляемую степенным рядом в области его сходимости. Очевидно,
, представляемую степенным рядом в области его сходимости. Очевидно, 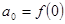 . Далее, последовательно применяем теорему о почленном дифференцировании ряда.
. Далее, последовательно применяем теорему о почленном дифференцировании ряда.  , откуда
, откуда  .
. 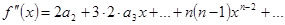 , откуда
, откуда 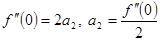 .
. 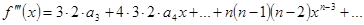 ,
,  и т.д.
и т.д.  .
.
Следовательно, при всех 
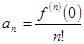 . Таким образом,
. Таким образом, 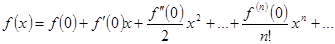 . Это можно сформулировать так: степенной ряд, сходящийся к
. Это можно сформулировать так: степенной ряд, сходящийся к 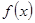 , представляет собой ряд Тейлора для своей суммы
, представляет собой ряд Тейлора для своей суммы 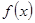 .
.
Если 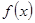 имеет производные произвольного порядка в точке
имеет производные произвольного порядка в точке  , то можно образовать соответствующий ей ряд Тейлора:
, то можно образовать соответствующий ей ряд Тейлора: 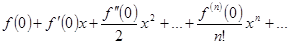 .
.
Важное замечание. Не всегда этот ряд сходится к самой функции 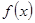 . Например, нетрудно доказать, что функция
. Например, нетрудно доказать, что функция  имеет производные произвольного порядка в точке
имеет производные произвольного порядка в точке  и все они равны 0, т.е.
и все они равны 0, т.е.  . Ряд Тейлора этой функции тождественно равен 0 и не совпадает с
. Ряд Тейлора этой функции тождественно равен 0 и не совпадает с 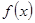 .
.
Необходимое и достаточное условие для того, чтобы ряд Тейлора функции 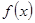 сходился к самой функции
сходился к самой функции 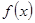 , можно сформулировать так: остаток
, можно сформулировать так: остаток  должен стремиться к 0 при
должен стремиться к 0 при  .
.