Доказательство.
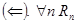 сходится Þ сходится
сходится Þ сходится 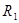 . Но
. Но 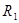 - это и есть исходный ряд.
- это и есть исходный ряд.
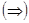 . Ряд сходится Þ существует
. Ряд сходится Þ существует 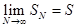 . Но
. Но 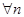 частичная сумма
частичная сумма 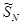 ряда
ряда  имеет вид
имеет вид 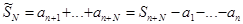 . Величина
. Величина 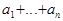 не зависит от
не зависит от  . Кроме того,
. Кроме того, 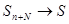 при
при  . Поэтому существует
. Поэтому существует 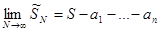 . Утверждение доказано.
. Утверждение доказано.
Итак, исследование сходимости ряда и исследование сходимости любого его остатка – эквивалентные задачи. Это означает, что при изучении сходимости достаточно рассматривать лишь члены ряда, начиная с некоторого номера. Это не влияет на сходимость. Изменится лишь сумма ряда.
Теорема. 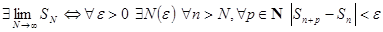 (1).
(1).
Примечание. Поскольку 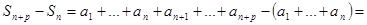
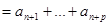 (2), неравенство (1) можно заменить на неравенство
(2), неравенство (1) можно заменить на неравенство  .
.
Следствие. (Необходимый признак сходимости ряда).
 . Действительно, при
. Действительно, при 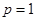 получаем неравенство
получаем неравенство 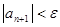 , выполняющееся
, выполняющееся  . Это значит, что
. Это значит, что 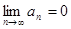 . Согласно этому следствию, мы получаем новое доказательство того, что ряд
. Согласно этому следствию, мы получаем новое доказательство того, что ряд  расходится при
расходится при  .
.
Важный пример, показывающий, что необходимый признак сходимости отнюдь не является достаточным.
Пример. Гармонический ряд  .
.  , т.е. общий член стремится к 0. Покажем, что этот ряд расходится. Используем критерий Коши. Следует доказать, что
, т.е. общий член стремится к 0. Покажем, что этот ряд расходится. Используем критерий Коши. Следует доказать, что 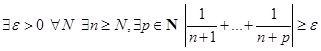 .
.
В качестве  выберем число
выберем число 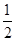 . Берем любое
. Берем любое  и любое
и любое 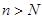 . Пусть
. Пусть  . Тогда
. Тогда 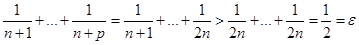 .
.
Теорема. Пусть сходятся ряды 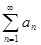 ,
, 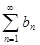 и
и  - постоянная величина. Тогда сходятся ряды
- постоянная величина. Тогда сходятся ряды  .
.
Доказательство. Обозначая частичные суммы  ,
, 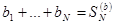 получим, что частичные суммы рядов
получим, что частичные суммы рядов  равны соответственно
равны соответственно 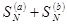 ,
, 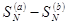 и
и  . Эти величины имеют пределы
. Эти величины имеют пределы 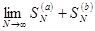 ,
, 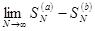 ,
, 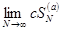 . Теорема доказана.
. Теорема доказана.