Ряды аналитических функций.

1. Понятие функционального ряда.
Пусть дана последовательность {u _k(z)} функций, z Î g. Выражение 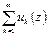- называется функциональным рядом, заданным в g.
Определение.Если при " z Î g, соответствующий числовой ряд сходится к определенному комплексному числу f(z), то в g определена функция, которая называется суммой функционального ряда, а сам ряд называется сходящимся в g.

r_n(z)=f(z)- 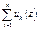- n-ый остаток ряда

Если ряд сходится в g, то

"e>0 $ N(e,z): | r_n(z)| <e для " n > N(e, z).

Пример.

- знакочередующийся ряд, сходится и признаку Лейбница, остаток ряда не превышает модуля следующего слагаемого

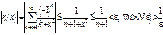
Необходимый и достаточный признак сходимости:
Критерий Коши: для "e>0 $ N(e ,z): | S_n+m(z)-S_n(z)| <e для "n > N и "m>0.
Вообще говоря, в каждой точке z Î g N свое: N=N(e ,z) и общего N для всей z может и не существовать.

2. Равномерная сходимость åu_k(z) в области g.

Определение. Если для "e>0 $ N(e) : | r_n(z)| <e для "n >N(e) и " z одновременно, то ряд åu_k(z) называется равномерно сходящимся к функции f(z) в g.
Обозначение: åu_k(z)=>f(z).

Критерий Коши (необходимое и достаточное условие равномерной сходимости).

Если для "e>0 $ N(e ): | S_n+m(z)-S_n(z)| <e для "n > N и "m>0 и " z одновременно, то ряд åu_k(z)=>f(z).
Доказательство.
Необходимость.

Пусть åu_k(z)=>f(z) "e >0 $ N(e): |f(z)-S_n(z)| <e /2 для "n>N(e) и "zÎg => и |f(z)-S_n+m(z)| <e /2 =>
=>| S_n+m(z)-S_n(z)| <e для "n>N и "m>0 и "zÎg.
Достаточность. Пусть для "e>0 $ N(e ): | S_n+m(z)-S_n(z)| <e для "n>N и "m>0 и "zÎg => 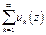сходится в "zÎg, т.о. в g определена f(z)= .

для "n>N(e) и "zÎg => |r_n(z)| <e для "n>N(e) и "zÎg. n

Признак Вейерштрасса (достаточный признак равномерной сходимости).
Если |u_k(z)|<a_k, a_k>0 для "k>N и "zÎg и Sa_k сходится, то Su_k(z)=>f(z) в g.
Доказательство.

Sa_k сходится => "e>0 $ N(e): 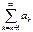<e для "n>N(e)

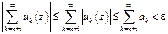
для "n>N(e) и "zÎg. n

Примеры.

1.

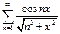
2. (оценить сверху значением функции в ее максимуме)

3. 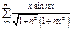(оценить сверху значением функции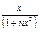в ее максимуме )

4. ()

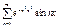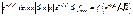3. Свойства равномерно сходящихся рядов.

Свойства равномерно сходящихся рядов:
Теорема 14.1. (непрерывность суммы) Пусть u_k(z)ÎС(g) и Su_k(z)=>f(z), тогда f(z)ÎС(g).
Доказательство.

u_k(z)=>f(z) Þ одновременно выполнены неравенства

|f(z+Dz)-S_n(z+Dz)|< e/3 и |f(z)-S_n(z)|< e/3 для "e>0.

u_k(z)ÎС(g) Þ для "e>0 и "N $ d>0:

при |Dz|<d

Þ |Df|=|f(z+Dz)-f(z)|£

£|f(z+Dz)-S_n(z+Dz)|+|S_n(z+Dz)-S_n(z)|+|S_n(z)-f(z)| £

£e/3+e/3+e/3=e для |Dz|<d , n>N.n

Примеры

1. 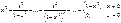Ряд из непрерывных функций сходится к разрывной функции, значит сходимость неравномерная

2. аналогично

Теорема 14.2. (возможность почленного интегрирования). Пусть u_k(z)ÎС(g) и Su_k(z)=>f(z), G кусочно- гладкий контур GÌg конечной длины L. Тогда .

Доказательство

u_k(z)=>f(z) Þ

для "e>0 $ N(e): | r_n(z) |<e/L для "n>N(e)

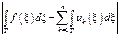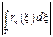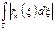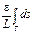=£<=en

Замечание. Эти два свойства равномерно сходящихся рядов с комплексными членами совершенно аналогичны свойствам равномерно сходящихся функциональных рядов с действительными членами.

Примеры.

1. Найти , если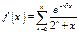

2. Является ли непрерывной функция

3.

4.

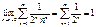
5.

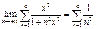
Теорема Вейерштрасса. Если u_k(z)ÎC^¥(g) и Su_k(z)=>f(z) в любой замкнутой подобласти области g то:

1. f(z)ÎC^¥(g).

2. 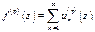, для "zÎg.

3. 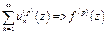"z Î".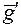

Доказательство
1. Рассмотрим произвольную z₀Îg и построим односвязную : z₀Î, в силу Теоремы 14.1 f(z)ÎС(g).

Рассмотрим произвольный контур GÌ. По Теореме 14.2 .

Т.о. для f(z) выполнены все условия Теоремы Морера Þ f(z)ÎC^¥(). В силу произвольности f(z)ÎC^¥(g).

Замечание. Т.к. r_n(z)=f(z)-S_n(z) Þ r_n(z) ÎC^¥(g).

2. Рассмотрим произвольную z₀Îg и произвольный контур GÌg. Обозначим .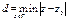

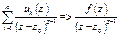для " zÎG, т.к.

По Теореме 14.2 это равенство можно проинтегрировать почленно

По Теореме 8.1.

.

В силу произвольности z₀ утверждение 2 доказано.

Замечание. r_n^(p)(z)=f^(p)(z)-S_n^(p)(z)=.

3. Рассмотрим "и G - замкнутый контур: ÌGÌg и "zÎи "xÎG |z-x|³d>0.

r_n(z) ÎC^¥(g) Þ для "zÎ.

u_k(z)=>f(z) Þ "e>0 $ N(e): , где L- длина G.

Тогда .

Т.о. получена равномерная оценка для остатка ряда для производных Þ .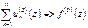

Пример.Ряд Sz^k/k² сходится равномерно в круге |z|£1, а ряд из производных Sz^k-1/k не может равномерно сходится в этом круг, т.к. он расходится при z=1. Ряд Sz^k-1/k равномерно сходится при |z|<1.

Для равномерно сходящихся функциональных рядов с действительными членами верна

Теорема 14.3. Пусть u_k(x) – непрерывно дифференцируемы на отрезке [a,b] и ряд, составленный из производных 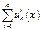- равномерно сходится на отрезке [a,b], тогда если ряд сходится хотя бы в одной точке cÎ[a,b], то он равномерно сходится на всем отрезке [a,b], его сумма 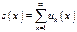непрерывно дифференцируема и .

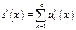Доказательство.

Пусть (непрерывна в силу равномерной сходимости ряда).

Найдем первообразную

для . Ряд сходится по условию теоремы Þ тоже сходится на всем промежутке.

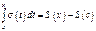
Левая часть равенства имеет производную по x Þ$S¢(x)=s(x) и

сходится равномерно, т.к. первый ряд справа сходится равномерно, а второй не зависит от x.

Примеры.

1. Равномерно сходящийся на всей действительной оси ряд 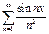дифференцировать нельзя, так как ряд из производных 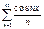расходится, например при x=0.

2. (1+1+1+1+…)¢=0+0+0+0+… Ряд, полученный в результате формального дифференцирования, сходится и даже равномерно, но дифференцирование не правомерно, т.к. исходный ряд расходится.

3. 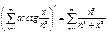почленное дифференцирование возможно в силу равномерной сходимости ряда из производных.

§15. Степенные ряды.

Определение. Степенным рядом назовем ряд вида c_n(z-z₀)ⁿ, z₀ -центр, c_n - коэффициенты - заданные комплексные числа. При z= z₀ ряд очевидно сходится. Это может быть единственная точка сходимости Sn!zⁿ, а также ряд может сходится на всей комплексной плоскости Szⁿ/n!. При исследовании степенного ряда важно установить область его равномерной сходимости. Как будет показано далее, область сходимости степенного ряда определяется видом его коэффициентов c_n.