Нули аналитической функции.
Определение. Пусть f(z)ÎC¥(g); f(z0)=0, z0Îg, тогда z0 - нуль аналитической функции.  Þ С0 =0. В этом случае
Þ С0 =0. В этом случае 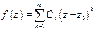
Если C1=…= Cn-1 =0, а Cn¹0, то z0 - нуль n-того порядка. В этом случае 
Заметим, что в нуле n-того порядка f(z0) = f ' (z0)=… = f(n-1)(z0) = 0, f(n)(z0)¹0 и f(z)=(z-z0)n×f1(z), где f1(z0) ¹0.
Если Cn=0 "n, то f(z)º0.
Примеры.
1) 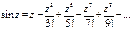 Точка z=0 - нуль первого порядка.
Точка z=0 - нуль первого порядка.
2) 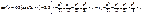 Точка z=0 - нуль второго порядка.
Точка z=0 - нуль второго порядка.
3)  Точка
Точка 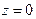 - ноль третьего порядка
- ноль третьего порядка
4) 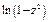 Точка
Точка 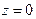 - ноль второго порядка
- ноль второго порядка
Теорема о нулях аналитической функции.
2.
Пусть f(z)ÎC¥(g) и $ 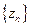 : (zi¹zk , все znÎg и f(zn)=0), имеющем предельную точку (точку сгущения) aÎg (
: (zi¹zk , все znÎg и f(zn)=0), имеющем предельную точку (точку сгущения) aÎg ( zn=aÎg). Тогда f(z)º0, для "zÎg ммой бесконечно убывающей геометрической прогрессии
zn=aÎg). Тогда f(z)º0, для "zÎg ммой бесконечно убывающей геометрической прогрессии  , ряд для исходной функции получается почленным интегрированием ряда для производной)
, ряд для исходной функции получается почленным интегрированием ряда для производной)
6.
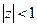
 Þ
Þ
" k 
В частности, при a=0.5 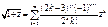
Доказательство.
Т.к. aÎg, то  , причем радиус сходимости этого степенного ряда R0 не меньше расстояния от a до ¶g
, причем радиус сходимости этого степенного ряда R0 не меньше расстояния от a до ¶g
f(z)ÎC¥(g)=> по непрерывности f(a)=0 => С0=0, т.о.
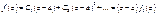
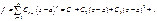
Новая функция f1(z) отличается от исходной одним множителем (z-a) => имеет те же нули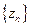 , что и f(z). По непрерывности f1(a)=0 => С1=0.
, что и f(z). По непрерывности f1(a)=0 => С1=0.
Продолжая в том же духе, получим Cn=0 "n. Это означает, что f(z)º0 "z: |z-a|<R0
Докажем, что f(z1)º0, для "z1Îg.
Соединим z1 и a кусочно-гладкой кривой L, целиком лежащей в g и отстоящей от ее границы ¶g на расстояние d>0.
Поскольку "z: |z-a|<R0 можно рассматривать, как предел последовательности нулей f(z), то в качестве нового центра разложения можем выбрать точку z=a1 – точку пересечения кривой L с окружностью |z-a|=R0. Проведя аналогичные рассуждения, получим, что f(z)º0 "z: |z-a1|<R1, где R1³d. Продолжая рассуждать подобным образом, покроем всю кривую L кругами, внутри которых f(z)º0. При этом точка z1 попадет внутрь последнего круга и тем самым f(z1)= 0.
Следствие. f(z)ÎC¥(g) внутри любой замкнутой подобласти  может иметь лишь конечное число нулей, иначе
может иметь лишь конечное число нулей, иначе 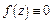 .
.
Пример. sin (1/z) )ÎC¥(g/0) имеет в конечной замкнутой области бесконечное число нулей {zn=1/pn}®0. Что не противоречит теореме, т.к. в z=0 нарушается аналитичность.
3. Теорема единственности определенной аналитической функции.
Теорема 22.1. Если f1 (z) и f 2(z) ÎC¥(g) и $ {zn}®aÎg, (zi¹zk) и f1(zn)=f2(zn ), то f1(z)ºf2 (z) для " zÎg.
Для доказательства достаточно при помощи теоремы о нулях установить, что функция h(z)=f1(z)-f2(z)º0 в g.
Следствия теоремы единственности.
В области g может существовать только одна аналитическая функция, принимающая заданные значения на
a) {zn}®aÎg, (zi¹zk) сходящейся последовательности различных точек.
b ) xÎgÌ g, кусочно-гладкой кривой g.
c) "zÎg'Ìg в произвольной подобласти области g.
Т.е. с этих множеств функцию f(z) можно аналитически продолжить, причем единственным способом.
На этом факте основано продолжение элементарных функций с действительной оси. В самом начале курса мы формально вели элементарные функции комплексного переменного (expz, sinz, cosz…) совпадение обозначений которых с функциями, заданными на действительной оси могло оказаться чистой случайностью.
Однако мы получили разложения в степенные ряды функций комплексного переменного


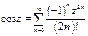
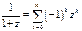 ,
, 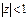
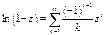
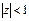
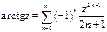
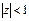
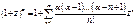
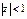
Эти ряды на действительной оси z=x совпадают с рядами Тейлора для элементарных функций действительного переменного, полученными в курсе анализа функций действительных переменных. Т.о. элементарные функции комплексного переменного совпадают со своими аналогами на действительной оси (или отрезках действительной оси). Поэтому мы можем утверждать, что их аналитическое продолжение на комплексную плоскость единственно, согласно теореме единственности (случай b – функции совпадают на кусочно-гладкой кривой).
Продолжение соотношений типа  c действительной оси также единственно, как продолжение функции
c действительной оси также единственно, как продолжение функции 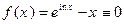 .
.
Теорема 22.2. На границе круга сходимости степенного ряда  лежит хотя бы одна особая точка аналитической функции
лежит хотя бы одна особая точка аналитической функции Доказательство (от противного)
Доказательство (от противного)