Если бы все точки границы были бы правильными, то

"x: |x-z₀|=R- граница круга сходимости

$r(x)>0: 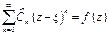"z |x-z|<r(x), т.е. задана строго 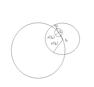положительная функция r(x)

Докажем, что для этой функции в любых двух точках границы круга сходимости выполнено неравенство:

.

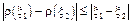Предположив, что это неравенство не выполнено, получим, например,

,

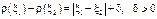но тогда круг 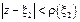лежит целиком внутри круга

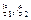
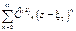Тогда степенные ряды с центром разложения в точках и совпадают в общей части кругов сходимост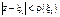и и 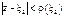и т.о. в силу единственности аналитического продолжения радиус круга сходимости ряда 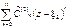больше, чем . Это противоречие и доказывает неравенство

.

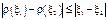Т.о. вещественнозначная функция 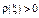- равномерно непрерывна на окружности |x-z₀|=R, и в силу ограниченности достигает своей нижней грани. Т.е. $x₀: , т.е. $x₀ - особая точка на границе круга сходимости.

заметим, что часть этого круга лежит вне круга сходимости исходного степенного ряда.

Следствие. Радиус сходимости степенного ряды аналитической функции равен расстоянию от центра разложения до ближайшей особой точки. Это можно использовать для определения радиуса сходимости, например, ряды

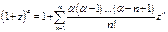
Центр разложения z=0, ближайшая особая точка z=-1 – точка ветвления функции .