Теоремы Мореры и Лиувилля.

 

Теорема Мореры. Если f(z)ÎC(g), g-односвязная и для " замкнутого gÌg: , то f(z)Î C^¥(g).

Доказательство. При условиях теоремы $ Î C^¥(g) (Теорема 6.1.), где z₀ и z- произвольные точки g, а интеграл берется по " пути внутри g, соединяющему эти точки. При этом F'(z)=f(z). Но производная аналитической функции сама является аналитической функцией (Теорема 8.1), в частности $ F"(z)= f '(z) ÎC(g).

 

Теорема Лиувилля. Если f(z)- аналитическая на всей комплексной области и $ M: |f(z)|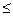M, f(z) º const.

 

Доказательство. Выразим значение f '(z) в произвольной точке z через значения функции на окружности радиуса R с центром в точке z

.

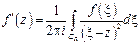На C_R: |x -z|=R. По условию теоремы $ M: |f(x)|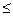M не зависимо от R=>

Устремив R®¥, получим |f '(z)|=0 Þ f(z)=const для " z.

Замечание. Отсюда, в частности следует, что $ z: |sin(z)|>1.