ЧИСТЫЙ ИЗГИБ КРИВОГО БРУСА

Для определения напряжений при чистом изгибе плоского кривого бруса, так же как для прямого бруса, считаем справедливой гипотезу плоских сечений. Определяя деформации волокон бруса, пренебрегаем напряжениями в радиальном направлении. Рассматриваем брусья с сечениями, симметричными относительно оси Оу, лежащей в плоскости кривизны бруса, и будем считать, что изгибающий момент приложен в той же плоскости.

На рисунке 344, а, б показан элемент бруса длиной ds с симметричным поперечным сечением. Ось Ох направим по нейтральной оси, вокруг которой поворачивается сечение.

Эпюра абсолютных удлинений волокон показана на рисунке 344, в, а эпюра относительных удлинений изображена на рисунке 344, г.

Абсолютное удлинение на высоте сечения изменяется по закону прямой линии, а относительное — по закону кривой линии (гиперболы). Объясняется это тем, что значение длины дуги dsp = ρdφ также меняется по высоте и поэтому для произвольного волокна, отстоящего от нейтрального слоя на расстоянии у, имеем

Считая, что волокна друг на друга не давят, по закону Гука найдем

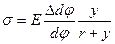(14.1)

При чистом изгибе нормальная сила отсутствует, поэтому

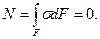
Или с учетом (14.1) получим

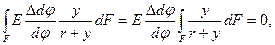
но так как множитель, стоящий перед интегралом, не может равняться нулю, то

(14.2)

Равенство (14.2) является условием для определения положения нейтрального слоя. Из равенства видно, что нейтральная ось в кривом брусе не проходит через центр тяжести, так как в последнем случае должен был бы равняться нулю статический момент 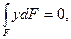как это было для прямого бруса (см. § 62).

Рисунок 344

Выразим теперь момент внутренних сил относительно нейтрального слоя через напряжения и приравняем его внешнему моменту, взятому по абсолютной величине:

(14.3)

 

Интеграл, входящий в равенство (14.3), можно представить в виде

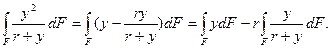
Второе слагаемое в полученном выражении согласно равенству (14.2) равно нулю, поэтому

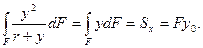(14.4)

где Sx = Fу₀ — статический момент площади поперечного сечения относительно нейтральной оси (у0 — расстояние от центра тяжести сечения до нейтральной оси).

Подстановка (14.4) в равенство (14.3) дает

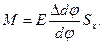
Следовательно,

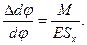(14.5)

Подставляя полученное выражение в формулу напряжений (14.1)

Рисунок 345

и учитывая, что r + у = ρ, т. е. равно расстоянию от центра кривизны до точки, в которой определяется напряжение, окончательно получим

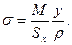(14.6)

Формула и; существенно отличается от формулы для прямого бруса, прежде всего тем, что в знаменатель входит переменная величина ρ, зависящая от у.

Эпюра напряжений в сечении кривого бруса изменяется по гиперболическому закону (рисунок 345). Наибольшие напряжения в сечениях, имеющих две оси симметрии, возникают в крайнем волокне, обращенном к центру кривизны. Знак напряжения, вычисленного по формуле (14.6), следует определять исходя из физического смысла.

Для того чтобы сравнить формулы для прямого и кривого брусьев, преобразуем формулу (14.6). Из (14.4) найдем

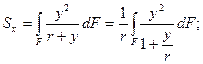
обозначим

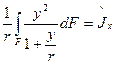
Этот интеграл назовем моментом инерции для сечения кривого бруса. Значок вверху в виде дуги служит отличительным знаком от обычного осевого момента инерции. Легко заметить, что при 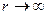момент инерции для кривого бруса в пределе совпадает с обычным осевым моментом инерции. Таким образом,

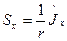(14.7)

Подставляя это выражение в формулу (14.6) и учитывая, что ρ=r+y, получим

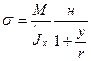
(14.8)

Если 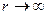, то формула (14.8) в пределе совпадает с обычной формулой для прямого бруса.

В § 114 дается сравнительная таблица результатов, получаемых по двум формулам: для кривого и прямого брусьев.