МЕТОД ЭЙЛЕРА ДЛЯ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКИХ СИЛ. ВЫВОД ФОРМУЛЫ ЭЙЛЕРА
Для исследования устойчивости равновесия упругих систем имеется несколько методов. Основы и техника применения этих методов изучаются в специальных курсах, посвященных проблемам устойчивости различных объектов, встречающихся в строительстве и машиностроении.
Наиболее универсальным является динамический метод, основанный на изучении колебаний системы вблизи заданного положения равновесия. Однако в курсах сопротивления материалов он обычно не изучается по двум причинам: во-первых, его применение требует специальных знаний в области динамики упругих систем, а во-вторых, и это главное, подавляющее большинство задач, встречающихся в инженерной практике, может быть решено более простым методом — методом Эйлера.
Метод Эйлера основан на анализе разветвления возможных форм равновесия упругой системы. Рассмотрим его идею более подробно на примере центрально-сжатого, идеально прямого стержня. При
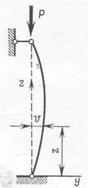Рисунок 356
|
малых сжимающих силах прямолинейная форма стержня является устойчивой. При больших силах, превышающих некоторое критическое значение, она является неустойчивой, а устойчивой будет криволинейная форма.
Таким образом, при Р > Ркр теоретически возможно существование двух форм равновесия. Наименьшее значение сжимающей силы, при котором наступает разветвление форм равновесия, называется критической силой. Следовательно, при критической силе наряду с исходной прямолинейной формой как бы возможна смежная, весьма близкая к ней искривленная форма. По определению Эйлера, критической силой называется «сила, требующаяся для самого малого наклонения колонны». Желающим более подробно ознакомиться с этим вопросом рекомендуем книгу В. В. Болотина «Неконсервативные задачи теории упругой устойчивости» (Физматгиз, 1961).
Для вывода формулы Эйлера рассмотрим шарнирно-опертый, центрально-сжатый стержень постоянного сечения (рисунок 356) в слегка отклоненном состоянии от прямолинейной формы.
Изгибающий момент в произвольном сечении равен
М = Рυ
Дифференциальное уравнение изгиба стержня запишется в следующем виде:
[‡‡‡]
или
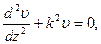(15.1)
где
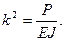(15.2),
Интеграл дифференциального уравнения (15.1) имеет вид
υ = Acoskz + Bsinkz. (15.3)
Для определения значений произвольных постоянных А и В используем граничные условия. Первое граничное условие: при z — 0 и v = 0 А = 0.
Следовательно, уравнение оси изогнутого бруса (15.3) примет вид
υ = Bsinkz. (15.4)
Таким образом, стержень изгибается по синусоиде. Второе граничное условие: при z =l и v = 0 Вsinkl = 0. Это условие выполняется в двух случаях:
1)B = 0; 2)sinkz = 0.
Первый случай нас не интересует, так как при В = 0 прогибы во всех точках равны нулю, следовательно, стержень остается прямым.
Второе условие sin kl = 0 дает kl = π, 2π, 3π, ..., nπ, учтя значение k (15.2), получим:
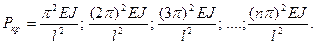
Итак, получено не одно, а множество значений критических сил. Каждой критической силе соответствует своя форма равновесия (рисунок 357). Подставляя найденное значение k в уравнение оси изогнутого бруса (15.4), замечаем, что при первой критической силе стержень изгибается по одной полуволне синусоиды, а при всех последующих число полуволн равно номеру соответствующей критической силы.
Интересно отметить, что равновесие, соответствующее первой форме изгиба, является устойчивым, а всем остальным — неустойчивым.
Для инженерных расчетов практический интерес представляет только наименьшая критическая сила
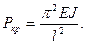(15.5)
Рисунок 357
Эту формулу более двухсот лет назад (в 1744 г.) впервые получил Леонард Эйлер, поэтому ее называют формулой Эйлера, а определяемую этой формулой критическую силу часто называют эйлеровой силой.
Из формулы Эйлера видно, что величина критической силы прямо пропорциональна жесткости и обратно пропорциональна квадрату длины стержня.
Для стержня, работающего в упругой стадии, критическая сила зависит только от геометрических размеров стержня и модуля упругости материала, но совершенно не зависит от прочностных характеристик материала, из которого изготовлен стержень. Так, например, она не зависит от сорта стали. Для стали Ст. 3 и для высокосортной стали модули упругости практически одинаковы, поэтому и критические силы также равны между собой. Два стержня с одинаковыми геометрическими размерами, но изготовленные из различных сталей и работающие в упругой стадии, теряют устойчивость при одной и той же критической силе.
Таким образом, выясняется резкая разница между работой стержня на сжатие и на растяжение. Предельная растягивающая сила непосредственно зависит от прочностных характеристик материала и потому различна для разных сортов стали, в то время как при сжатии в пределах упругости наблюдается совершенно иная картина.
Предельная растягивающая сила не зависит от длины стержня, в то время как при сжатии она быстро падает с увеличением длины.
Продольный изгиб сжатых стержней особенно опасен потому, что он наступает внезапно, и поэтому его трудно предупредить в тех конструкциях, в которых неправильно назначены размеры сжатых элементов. В растянутых стержнях признаки опасного состояния часто наступают задолго до разрушения, а в сжатых стержнях каких-либо заметных признаков возможной потери устойчивости, как правило, установить не удается.
Все сказанное заставляет обратить особое внимание на устойчивость сжатых стержней.
При выводе формулы Эйлера было установлено, что стержень, шарнирно опертый по концам, изгибается по синусоиде, а найти численные значения прогибов не удалось. (Величина постоянной интегрирования В осталась неопределенной.) Это связано с тем, что было использовано приближенное уравнение
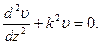
Если применить точное дифференциальное уравнение
(15.6)
то при Р > Ркр можно найти прогибы стержня. Интегрирование уравнения (15.6) проводится с помощью сложных специальных функций. Изучение этого вопроса выходит за рамки нашего курса.