Так как в балке выделяются два участка для М (х), необходимо составить дифференциальные уравнения для каждого участка

7.8. Путем интегрирования дифференциальных уравнений изогну­той оси с применением метода уравнивания произвольных постоянных определить величину наибольшего прогиба в пролете и опускание точки приложения силы для балки, изображенной на рисунке. Найти также углы поворота опорных сечений А и В.

Решение. Опорные реакции равны:

„ Ра + М₀, Р(1+а) + М_0/

А —---- 1--- У (вниз), В——-———---- 5 (вверх).

l I

Так как в балке выделяются два участка для М (х), необходимо составить дифференциальные уравнения для каждого участка. Решение упрощается, если

выражения моментов на каждом участ­ке составлять, отсчитывая абсциссы сечений /—/ и 2—2 от одного начала координат (например, от точки Л) и рассматривая каждый раз одну и ту же отсеченную часть балки (у нас—левую). Тогда

М_х = —Ах,

М₂ = — Ах--В(х—1) + М₀. Интегрирование будем вести без раскрытия скобок, для второго участ-

ка— по переменной (х — I), обращающейся в нуль при х=1. ото скажется лишь на величине произвольных постоянных, приводя к уравниванию соответ­ствующих постоянных для обоих участков. Получим:

Первый участок Второй участок

EJyl = — Ax EJy'₂ = — Ах+В {х—/) + М₀ {х—1)°

EJy'^-^ + Сг (I) EJy'₂ = -^+^B{X-^l)2+M₀(x-l) + C₂ (III)

E/^-^ + C^+D, (И) EJy^-^ + ^l + Щ^-,

+ C₂x + D₃ (IV)

Из уравнений (II) и (IV) видно, что изогнутая ось балки состоит из двух кривых. Так как при упругой деформации ось балки представляет собой не­разрывную плавную линию, то в точке сопряжения кривых (точка В) они должны иметь общую касательную и общий прогиб:

1) при х = 1 y'i — у'г, и 2) при x = l f/i = t/₂-

По первому условию из (I) и (III) получим С₁ — С₂ = С. Из второго усло­вия по (II) и (IV) найдем D_l^=D₂=^:D. Значения произвольных постоянных С и D определяются из условий закрепления балки на опорах Л и Б, где прогибы равны нулю:

3) при х — 0 уi = 0 и, следовательно, D = 0;

Л/^

4) при x = l y_l = y_i~O, откуда C — —z~ (из (II) или из (IV)).

Величина наибольшего прогиба в пролете найдется из уравнения (II).

Если У1 = {/_тах> ^Т0 У' — 0- Приравняв (I) нулю, найдем необходимое значение х,
соответствующее у_тах:

_п Ах* . АР I

О=—2~ + v откуда *=yv

Pa + M0 /з Pa+MQ /з =Ра + М (Ра + М0)/2 Величину прогиба в сечении под силой найдем из уравнения (IV) при x=l + a и у… Pa*(l--a) + MQal

О 0

XXX

3) EJy'='_idx^dx'_iq(x)dx + ^ + C₂x + C_3t

0 0 0

x x x x

4) EJy= J dx J dx J dx J q (x) ^т^ + ^ + ^+С₄.

0 0 0 0

Значения входящих в эти уравнения произвольных постоянных определя­ются из условий в начале координат при х — 0. Используя равенства (1) и (2), получим: С_х = EJy_(x = о = Q (* = 0) = -Ро. ^2 = EJy_(x = ₀> = М_о. Кроме того, при х = 0 C_i = EJy_lXm._Oi = EJQ_o nC_t = EJy_{x=0)=EJf_(t.

Таким образом, произвольные постоянные интегрирования являются на­чальными параметрами, т. е. геометрическими и силовыми факторами при х = 0, чем определяется и их размерность: f_& и 8₀—прогиб и угол поворота начального сечения, а Р_о и М_о — сосредоточенная сила и момент в начале координат.

Уравнение изогнутой оси через начальные параметры напишется так:

y = fo + %^ij^f + ^ + l^l 4(x)dA (a)

L 0 0 0 0 J

В случае равномерно распределенной нагрузки q (х)=q₆=const и послед­ний член уравнения после четырехкратного интегрирования получит значение

■^°^x ■, а уравнение (а) примет вид

y-fo + QoX + _Tj L-2- + ~6~ ⁺ ~2^J ' ^(б)

Воспользуемся им для определения перемещений в заданной балке. Так как в начале координат (точка Л) нет ни силы, ни момента, т. е. Р_о = 0 и М_о = 0, а нагрузка q_o = —q (направлена в сторону отрицательной оси у), то

уравнения прогибов и углов поворота примут вид

v _ f JL R v ^qX* л,' А ^

Начальные параметры f₀ и 0_О определим из условия закрепления балки в сечении В: при х = / у = 0 и при х = 1 у' = 0, откуда 6₀ = -^гу-=9_л и

Oil и

'° ~" 8£У ~ '^А'

При рациональном выборе начала координат решение может быть упро­щено. Рекомендуется решить эту же задачу, приняв начало координат в точке В и направив ось х влево. Как изменятся при этом начальные параметры?

Ответ: /₀=0; 6₀ = 0; Ж_о=-^_; P₀ = ql>, 6л = -^; ^JA~ 8EJ'

 

7.17. Пользуясь методом начальных параметров, определить величину наибольшего прогиба и углы поворота опорных сечений

деревянной балки, изображенной на рисунке. Сечение балки — пря­моугольник со сторонами £=15 см и /г = 20 см, пролет / = 3а = 6 м. Интенсивность нагрузки, приложенной на длине 2а, q — 0,3 т/м.

4 2

Решение. Опорные реакции: А = -^ qa_t B = -^-qa. Начало координат при-

О о

мем в точке А.

Для балки, разделенной на два или более участков, при нагружении ее силами, парами и равномерно распределенной нагрузкой общее уравнение изогнутой оси может быть написано в виде

,__ 1 [M_t(x-a_OT)² Pi(x-a_p)3 ftfr-Qg)⁴!

~*~ EJ [ 2! **" 3! ⁱ 4! J*

Здесь /₀, 0_O' M_o и Р_о — начальные параметры (см. задачу 7.10); ^ — интен­сивность равномерно распределенной нагрузки на первом (от начала коорди­нат) участке; Mi, Pi, q-_t — силовые факторы, появляющиеся в начале второго (и каждого последующего) участка при х — щ. Левая часть равенства, отде­ленная вертикальной чертой, представляет собой уравнение изогнутой оси в пределах только первого участка; все уравнение в целом описывает кривую только последнего участка балки (в нашем случае —второго). Следовательно, как и в задаче 7.8, у₂ = У1 + У_ДОп- Из этих соображений нагрузку q₀ первого участка следует продолжить до конца балки, восстановив нарушенную схему нагружения добавочной нагрузкой на втором участке q_t = —q_0> направленной вверх (см. рисунок).

В рассматриваемой балке начальные параметры (точка Л):

/о = 0, М₀ = 0, P₀ = A = ~qa;

нагрузки: q_o = — q, Mi = 0, P_f = 0, q_t — q (a_q = 2a). Уравнение упругой линии примет вид

y-W-r Ej [З 6 24 У i"¹" 24E1 '

Значение начального параметра 0_О найдем из условия равенства нулю про­гиба на опоре В 0/ = 0 при х = 3а). Подставляя х = 3а, получим

0= е₀. За + ^-[4_Яа (За)з-£ (За).+ Щ откуда 9₀— |-g-.

Окончательный вид уравнений прогибов и углов поворота:

1 / 8 - , 2 , qx* , а(х-2а)⁴

1 / 8 , . 2 „ qx* , д{х-2а)*
■ ^y==-Er[—9^qa4-li^qaX—6-)_х+ 6EJ • ^(б)

Для отыскания наибольшего прогиба надо найти абсциссу х, при которой у —г/_тач, т. е. у' = 0. В балках рассматриваемого типа наибольший прогиб располагается около середины пролета, поэтому рассматриваем только часть уравнения (б), относящуюся к первому участку:

Зг-4«^в'+!*'*-⁰-

Решая уравнение методом последовательного подбора, найдем # = 1,445а. Подставляя х в уравнение (а), для первого участка получим

* 1 Г 8 2 (1,445а)⁴] 0,8да«

^ах—Щ-[—э-^-1,445а+_¥?а(1,445а)3-а^ ₂₄ j -,--—.

Для получения числового ответа подсчитаем жесткость балки:

ииъ 15-20³ J = — = ^ = 10 000 см Е J = ЫО⁵ • 10⁴ = 10⁹ /сгсм².

Следовательно,

0,8да⁴ 0,8- 0,3- 2⁴-10» _{0 ол}
/max =------- ЁГ------------ ГПо^------ — 3,84 см.

Углы поворота опорных сечений: 6д = ул:-о>» ®в — ух-за)- Из (б) имеем

е^-⁸^⁸'⁰-^{3 23}-¹⁰⁷^-0,0213, e_R=M₌₌⁷.°^²³^!₌₌ooi87

^л 9ЈJ 9-109 ^в 9ЈJ 9 109 "."А»'-

9.1. Раскрыть статическую неопределимость стальной балки, показанной на рисунке, определить опорные реакции, построить эпюры изгибающего момента и поперечной силы, подобрать двутав­ровое сечение балки при допускаемом нормальном напряжении

lbOO кг/см% определить ве­личину наибольшего проги­ба балки, сравнив с наи­большим допускаемым про­гибом, равным 0,002 про­лета балки.

Решение. Из уравнений ста­тики устанавливаем следующие зависимости:

Н_в = 0, A-^B = qa, (1) 3Ba-M_B = M₀ + ^q~. (2)

При двух уравнениях—три неизвестных. Применим при раскрытии статической неопре­делимости метод интегрирова­ния дифференциального урав-

нения изогнутой оси балки с использованием приема уравнивания произволь­ных постоянных интегрирования (см. решения задач в § 22). Начало координат примем в точке В, в защемлении балки, чтобы произвольные постоянные С и D оказались равными нулю. Составляем дифференциальное уравнение упругой линии и интегрируем его дважды:

EJy"=Bx-M_B-M₀(x-2a)0 — q ⁽*~^2a)2, EJy' = B^-M_Bx-M₀(x-2a)-qЈ=^ + C,

Записываем следующие три условия для определения неизвестных величин: #! = (), {/i = 0; отсюда D = 0; х₁₌=0, j/i = 0; » С = 0, х₂ — 3а, 1/2 = 0;

подставив это значение х₂ в уравнение прогибов, получим следующую зави­симость:

9Ba-9M_B = M₀ + ^L. (3)

Для определения величины М_в решаем совместно уравнения (2) и (3):

(2) ЪВа-М_в = М₀+^~ -3

(3) 9Ва-Ж_в = М₀+^-

M_B^j М₀--^да'" = ~ + -^ = ²'^т ™-

Далее из уравнений (2) и (1) находим £=1,43 т и А = 2,57 г.

Обычными приемами строим эпюры поперечной силы и изгибающего мо­мента (схемы б и б). Наибольший изгибающий момент М_тах = 3,14 гж. Подби-

М 314 000 _1П. . „ ., _ОЛ

раем размеры балки: W =-т—.г = .„„„ = 1% см³. Нужен двутавр № 20а:

W == 203 еж³, J = 2030 см EJ = 4,06 • Ю⁹ кгслР.

Прежде чем вычислять перемещения, рекомендуется переписать уравнения углов поворота и прогибов, подставив в них все известные числовые величины:

EJy'= 0,715х*-2,56х —2 (х — 4)—~{x — i) (I)

О

£/г/ = 0,238х³— 1,28х² — (х—4)² —^(* — 4)⁴. (II)

Приемами, объясненными в § 22, определяем, что сечение с наибольшим прогибом находится на правом участке балки и имеет абсциссу x_ft = 3,58 м.

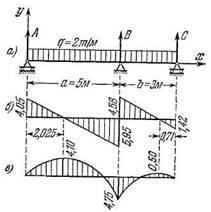
Это значение подставляем в уравнение (II) и устанавливаем, что наибольшая величина прогиба f=l,35 см, т. е. на 12% больше допустимой: [fj= 1,2 см. Приняв вместо двутавра № 20а следующий по порядку двутавр № 22 (J =2550 еж⁴, 1Г = 232 ел*³), снизим величину наибольшего прогиба до 1,18 см. Наибольшие нормальные на­пряжения в опасном сечении умень­шатся при новом профиле до 1355 кг/см².

9.2. Раскрыть статическую неопределимость стальной дву­тавровой балки, показанной на рисунке, определить опорные реакции, построить эпюры попе­речной силы и изгибающего мо­мента, подобрать сечение балки

при допускаемом нормальном напряжении, равном 1600 кг/см², и вычислить величину прогиба в сечении, отстоящем на 2 At от опоры А.

Решение. Составляем уравнения статики:

A + B + C = q(a + b), (1)

_{А {а + Ь}) + ВЬ-ЯЩ^-=0. _(2|

Для раскрытия статической неопределимости применим дважды общее уравнение прогибов:

в сечении В

в сечении С

ЕЫ_Аа + Ь_{) +} АЦ^+В^-^" + ^ЬУ .р. ₍₄

Решив все четыре уравнения, получим Л = 4,05 г, 6=10,53 т и С= 1,42 7 Эпюры поперечной силы и изгибающего момента построим обычными ' при­емами (схемы б и б).

Необходимый момент сопротивления сечения

_М_ ₌ 475000 [о] 1600 ~*" ^см-

Подходит двутавр № 24: W = 289 см?, 7 = 3640сж⁴, £/ = 3640-2-10⁶ =-= 6,9-10⁹ кгсм².

Для вычисления любого перемещения нужно определить сначала из уоав-

нения (3) величину £ДЬ (учтя, что А =4,05 т):

^ b ^ 24 b ^

, 2-125_ 155 ,
⁺ 24 ------- ~2Т ™'-

Для определения искомого про­гиба подставляем в общее уравнение прогибов значение х = 2 м:

9.94

------ 24" = 8,85 тм*.

Отсюда «/ = 8,85:6,9 = 1,28 см.

9.5. Раскрыть статическую неопределимость стальной двутавро­вой балки, показанной на рисунке, построить эпюры Q и М, подобрать сечение при [а] =1600 кг/см² и определить величину прогиба конца консоли.

Решение. Применим способ Максвелла — Мора. За лишнюю неизвестную примем реакцию А. Основная статически определимая балка показана на схе­ме б. Эту балку загружаем дважды: заданной нагрузкой и силой А (схема в) и единичной силой Р°=1 (схема г). Интеграл Мора, выражающий прогиб

в сечении А, должен быть равен нулю:

J М(х) >М° dx = 0 (i)

Левый участок балки не рассматриваем, так как на этом участке изги­бающий момент от единичной нагруз-

ки равен нулю.

На втором участке

М (х) = Лх-⁹⁽*^^а)2',Мо = Р°х = *,

^A^dx-^^Lxdx = 0.
о о

Отсюда А = 17 т. Эпюры Q и М по­строены на схемах д и е. | Mmax | = = 8 тм. Нужен момент сопротивле­ния № = 500 см³. Подойдет двутавр № 30а.

Для определения прогиба при составлении интеграла Мора прикла­дываем в конце консоли силу Р°=1 и от этого же места ведем отсчет абсцисс текущих сечений, как это по­казано на схеме ж).

EJy =

l+a l+a

= С ^-xdx+ ^ A(x — a)xdx.

А

Взяв интеграл, после подстановок по­лучим EJy= 13,33 тм³, г/ р^0,86 см, т. е. перемещение направлено вниз, по направлению силы Р°.