Свойства предела функции
Свойства предела функции
Сформулируем и приведем для примера доказательства некоторых теорем с использованием определений предела по Коши или по Гейне. 1. Функция имеет конечный предел при тогда и только тогда, когда , где -… 2. Теорема (о единственности предела). Если и , то .Что касается свойств непрерывных функций, то ограниченность непрерывной функции в окрестности точки , непрерывность линейной комбинации, произведения и частного (при условии отличия от нуля знаменателя в точке ) двух непрерывных функций являются тривиальными следствиями соответствующих свойств предела функции.
Для примера докажем утверждение о непрерывности суммы непрерывных функций.
Утверждение. Пусть функции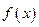 
и 
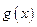непрерывны в точке 
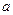. Тогда их сумма 
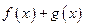также будет непрерывной в точке .
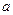Доказательство. 
Имеем 
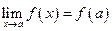и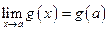 
. Тогда 
.
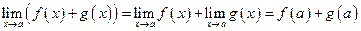Докажем вариант теоремы о предельном переходе в неравенстве для непрерывных функций.
Теорема (о сохранении знака непрерывной функцией). Пусть функция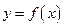 
непрерывна в точке 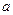и пусть 
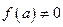. Тогда 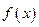сохраняет знак в некоторой окрестности точки .
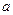Доказательство. 4Предположим для определенности, что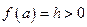 
. Положим 
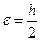. Из непрерывности функции 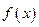в 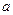следует, что существует окрестность 
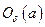, в которой выполнено неравенство 
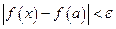. Тогда для 
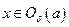будет верно
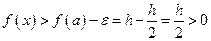.3
Упражнение. Пользуясь теоремами об арифметических действиях с пределами функций сформулируйте и докажите теорему о непрерывности линейной комбинации непрерывных функций, теоремы о непрерывности произведения и частного.