Предел сложной функции

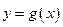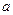Теорема (о пределе сложной функции). Пусть функция , определенная в проколотой окрестности точки , имеет предел 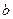при :

. (1)

И пусть функция 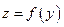определена в некоторой окрестности точки 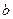, содержащей , и непрерывна в точке .

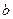Тогда сложная функция 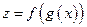определена в и существует предел

. (2)

(Другими словами, ).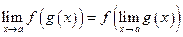

Доказательство. 4Фиксируем произвольное . Из непрерывности функции 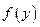в точке 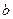следует

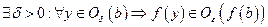, (3)

а из существования предела (1), что

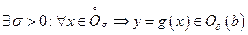. (4)

Объединяя (3) и (4), получим

Существование предела (3) доказано. 3

Следствие. Пусть функция 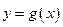непрерывна в точке 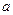, а функция 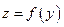непрерывна в точке . Тогда сложная функция 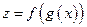будет непрерывной в точке .

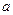Условия непрерывности внешней функции в точке 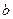существенно.

Пример. Пусть , а

Тогда и , в то время как

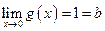и .

Первый замечательный предел

Теорема (о первом замечательном пределе). Справедлива формула

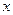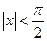Доказательство. 4Мы будем использовать школьное определение как ординаты точки при повороте (с центром в начале координат) на угол радиан. Так как нас интересует случай , то можно считать, что , а поскольку функция 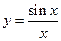четная, то достаточно рассмотреть углы из первой четверти: .

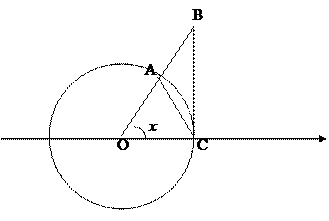Из геометрических соображений ясно, что

то есть

или .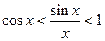

Так как

то по теореме о предельном переходе в двух неравенствах получим