Производная сложной функции
Теорема. Пусть функция 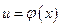 имеет в некоторой точке производную
имеет в некоторой точке производную 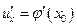 , а функция
, а функция 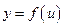 имеет в точке
имеет в точке 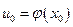 производную
производную 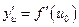 .
.
Тогда сложная функция 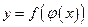 в точке
в точке 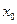 также имеет производную
также имеет производную 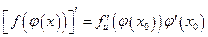 , или, короче
, или, короче  .
.
Доказательство. Придадим 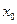 произвольное приращение
произвольное приращение 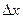 , пусть
, пусть  - соответствующее ему приращение функции
- соответствующее ему приращение функции  :
: 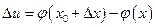 , а
, а 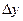 - приращение функции
- приращение функции 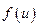 , вызванное
, вызванное  :
:  . Тогда
. Тогда
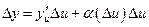 ,
,
где  - бесконечно малая при
- бесконечно малая при  . Доопределим функцию
. Доопределим функцию 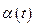 в нуле, положив
в нуле, положив 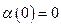 . Разделим последнее равенство на
. Разделим последнее равенство на 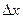 :
:
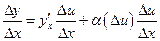 . (1)
. (1)
Так как функция 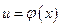 непрерывна в
непрерывна в 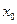 , то при
, то при 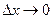 будет
будет , а значит, и
, а значит, и  (мы воспользовались теоремой о пределе сложной функции). Переходя в равенстве (1) к пределу при
(мы воспользовались теоремой о пределе сложной функции). Переходя в равенстве (1) к пределу при 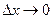 , получим
, получим  .
.
Занесем выведенные нами формулы в таблицу: