Касательная; геометрический смысл производной и дифференциала.
Определение. Касательной к графику функции  в точке
в точке  называется предельное положение секущей, проведенной через точки
называется предельное положение секущей, проведенной через точки  и
и 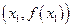 при
при 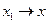 .
.
Все описанные секущие проходят через одну точку, а при 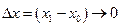 их угловые коэффициенты (тангенсы углов наклона их к оси
их угловые коэффициенты (тангенсы углов наклона их к оси  ) стремятся к определенному числу – угловому коэффициенту касательной.
) стремятся к определенному числу – угловому коэффициенту касательной.
Пусть 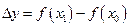 , тогда угловой коэффициент секущей равен
, тогда угловой коэффициент секущей равен  , а его предельное значение при
, а его предельное значение при 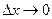 (если оно существует) совпадет с производной функции
(если оно существует) совпадет с производной функции  в точке
в точке 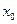 :
:
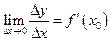 .
.
Уравнение касательной в таком случае выглядит следующим образом:
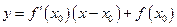 .
.
Следовательно, геометрический смысл производной  – это тангенс угла наклона к оси
– это тангенс угла наклона к оси  касательной, проведенной к графику функции
касательной, проведенной к графику функции  в точке
в точке  .
.
Обратимся к геометрическому истолкованию понятия дифференциала. Итак,
 .
.
Нетрудно заметить, что это – приращение ординаты касательной, соответствующее приращению абсциссы 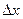 .
.
Учитывая тот факт, что дифференциал является линейно функцией от приращения независимой переменной, и что разность между приращением функции и дифференциалом есть бесконечно малая величина по сравнению с 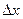 , мы можем сделать вывод, что дифференциал – главная, линейная часть приращения функции.
, мы можем сделать вывод, что дифференциал – главная, линейная часть приращения функции.