Функции
Пусть заданы два множества  и
и 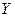 .
.
Говорят, что имеется функция, определенная на  со значениями в
со значениями в 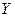 , если в силу некоторого закона
, если в силу некоторого закона  каждому элементу
каждому элементу  ставится в соответствие единственный элемент
ставится в соответствие единственный элемент  (обозначается
(обозначается 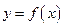 ).
).
Множество  называется областью определения функции, а множество
называется областью определения функции, а множество  всех значений функции, которые она принимает на элементах множества
всех значений функции, которые она принимает на элементах множества  называется множеством значений
называется множеством значений  :
:
 .
.
Функция  называется также отображением множества
называется также отображением множества  на множество
на множество 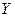 . Мы будем употреблять следующие обозначения:
. Мы будем употреблять следующие обозначения:
 .
.
Существует несколько способов задания функции.
Аналитический способ, когда функция задается одним или несколькими аналитическими выражениями. Например,  или
или

При табличном способе функция задается таблицей, содержащей значения аргумента и соответствующие значения функции. Например,

| 2,5 | 3,5 | 4,5 | ||||

| 6,25 | 12,25 | 20,25 |
Функцию можно также представлять графиком.
Графиком функции  называется подмножество
называется подмножество  прямого произведения
прямого произведения  , элементы которого имеют вид
, элементы которого имеют вид  , то есть
, то есть
 .
.
Задание. Расскажите, как соотносится график функции 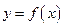 с графиками функций
с графиками функций  ,
,  ,
, 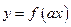 ,
,  ,
, 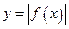 ,
,  .
.
Также задавать функцию можно словесно. В последнем случае функция описывается правилом ее составления, например, функция Дирихле:

Вспомним основные свойства функций.
Определение. Функция 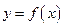 называется возрастающей (убывающей) на промежутке
называется возрастающей (убывающей) на промежутке  , если
, если  из
из  следует
следует  (
( - возрастающая,
- возрастающая,  - убывающая). Такие функции называются строго монотонными.
- убывающая). Такие функции называются строго монотонными.
Неубывающей (невозрастающей) называется функция 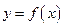 , если
, если  из
из  следует
следует  .
.
Пример. Функция  - неубывающая, а функция
- неубывающая, а функция  - невозрастающая.
- невозрастающая.
Все эти функции называются монотонными.
Определение. Функция 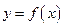 называется периодической с периодом
называется периодической с периодом  , если для всех
, если для всех  из области определения функции
из области определения функции  . Периодом называется наименьшее положительное значение
. Периодом называется наименьшее положительное значение  .
.
Например, функция 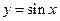 - периодическая с периодом
- периодическая с периодом  .
.
Определение. Функция 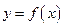 называется четной, если
называется четной, если 
 и нечетной, если
и нечетной, если 
 . Функция, не являющаяся ни четной, ни нечетной называется функцией общего вида.
. Функция, не являющаяся ни четной, ни нечетной называется функцией общего вида.
Определение. Функция 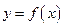 называется ограниченной (ограниченной сверху, ограниченной снизу) на множестве
называется ограниченной (ограниченной сверху, ограниченной снизу) на множестве  , если множество ее значений
, если множество ее значений  ограничено (соответственно, ограничено сверху или снизу).
ограничено (соответственно, ограничено сверху или снизу).
Запишем определения ограниченности функции с помощью кванторов:
ограниченность: 
 .
.
ограниченность сверху: 
 .
.
ограниченность снизу: 
 .
.
Задача. Доказать, что функция  - ограничена, функция
- ограничена, функция  - ограничена сверху, но не ограничена снизу, а функция
- ограничена сверху, но не ограничена снизу, а функция  - ограничена снизу, но не ограничена сверху.
- ограничена снизу, но не ограничена сверху.