Обратная функция.
Пусть функция  осуществляет взаимно однозначное отображение множества
осуществляет взаимно однозначное отображение множества  (области определения) на множество
(области определения) на множество 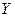 (множество значений).
(множество значений).
Обратной к функции  называется функция
называется функция  с областью определения
с областью определения 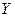 и множеством значений
и множеством значений  такая, что
такая, что  , если
, если 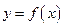 .
.
Видим, что так определенное отображение  само является биективным, и обратное к нему отображение совпадает с
само является биективным, и обратное к нему отображение совпадает с  . Отображения эти называются взаимно обратными, и справедливы тождества
. Отображения эти называются взаимно обратными, и справедливы тождества 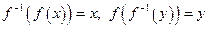 .
.
Пример. Рассмотрим функцию
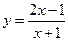 (3)
(3)
с областью определения  и множеством значений
и множеством значений 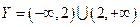 . Для любого
. Для любого  уравнение (3) имеет единственное решение
уравнение (3) имеет единственное решение
 . (4)
. (4)
Уравнение же  не имеет решений.
не имеет решений.
Следовательно, функция  с областью определения
с областью определения 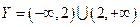 и множеством значений
и множеством значений  является обратной к (3).
является обратной к (3).
График функции  будет симметричен графику
будет симметричен графику 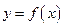 относительно биссектрисы I-III координатных углов.
относительно биссектрисы I-III координатных углов.
Задание. Постройте графики функций (3), (4) и функции  .
.
Задание. Вспомните, как выглядят графики функций  ,
, 
 , а также обратных тригонометрических функций.
, а также обратных тригонометрических функций.
Теорема. Если функция 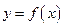
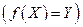 монотонно возрастает (убывает) на
монотонно возрастает (убывает) на  , то обратная к ней функция
, то обратная к ней функция  также будет монотонно возрастать (убывать) на
также будет монотонно возрастать (убывать) на 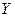 .
.
Доказательство. 4 Из монотонности функции следует, что если 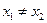 , то
, то 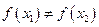 , поэтому каждое свое значение функция принимает только один раз, то есть
, поэтому каждое свое значение функция принимает только один раз, то есть  осуществляет взаимно однозначное соответствие между множествами
осуществляет взаимно однозначное соответствие между множествами  и
и 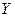 , и существует обратная функция
, и существует обратная функция 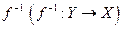 .
.
Для определенности предположим, что 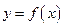 возрастает на
возрастает на  . Покажем, что
. Покажем, что  возрастает на
возрастает на 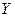 . Возьмем произвольные
. Возьмем произвольные  , пусть
, пусть 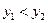 и пусть
и пусть  (то есть
(то есть 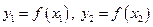 ). Если
). Если  , то и
, то и 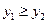 , что неверно, поэтому
, что неверно, поэтому 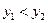 . Следовательно,
. Следовательно,  тоже возрастающая.
тоже возрастающая.
Случай убывания доказывается аналогично. 3